Question

（本题满分16分）已知函数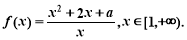

（1）当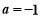时，判断并证明函数的单调性并求的最小值；

（2）若对任意，都成立，试求实数的取值范围.

 

Answer 1

（1）单调递增，2；（2）.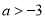

【解析】

试题分析：

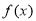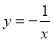解题思路：（1）先将的表达式进行化简，利用与在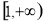都为增函数判断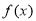的单调性，再用函数的单调性定义进行证明，进而求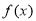的最小值；（2）因为父母恒为正，所以只研究分子的符号即可，采用分离常数法进行求解.

规律总结：不等式恒成立问题，一般思路将常数进行分离，将其转化为求函数的最值问题.

试题解析：（1）当a＝－1时f（x）＝，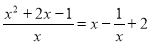

对任意，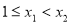

∵，∴∴

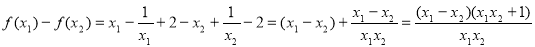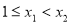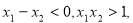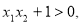
∴f（x1）－f（x2）<0，f（x1）<f（x2）

所以f（x）在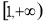上单调递增

所以x＝1时f（x）取最小值，最小值为2

（2）若对任意x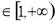，f（x）>0恒成立，则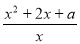>0

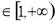对任意x恒成立，所以x2＋2x＋a>0对任意x恒成立，

令g（x）＝x2＋2x＋a， x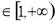

因为g（x）＝ x2＋2x＋a在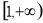上单调递增，

所以x＝1时g（x）取最小值，最小值为3＋a，

∵ 3＋a>0，∴ a>－3.

考点：1.函数的单调性与最值；2.不等式恒成立问题.