
设函数 ,给出以下四个命题:①当c=0时,有
,给出以下四个命题:①当c=0时,有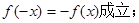 ②当b=0,c>0时,方程
②当b=0,c>0时,方程 ③函数
③函数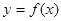 的图象关于点(0,c)对称 ④当x>0时;函数
的图象关于点(0,c)对称 ④当x>0时;函数 ,
, 。其中正确的命题的序号是_________。
。其中正确的命题的序号是_________。
1.2.3
解析试题分析::①c=0,f(x)=x|x|+bx,f(-x)=-x|-x|+b(-x)=-f(x),故①正确
②b=0,c>0,f(x)=x|x|+c= x2+c,x≥0
-x2+c,x<0
令f(x)=0可得x=-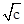 ,故②正确
,故②正确
③设函数y=f(x)上的任意一点M(x,y)关于点(0,c)对称的点N(x′,y′),则x=-x’,y=2c-y’代入y=f(x)可得2c-y′=-x′|-x′|-bx′+c⇒y′=x′|x′|+bx′+c故③正确
④当x>0时;函数 ,是开口向上的二次函数,那么由于对称轴的正负不定,因此
,是开口向上的二次函数,那么由于对称轴的正负不定,因此 错误,应该是不确定的。故填写1.2.3
错误,应该是不确定的。故填写1.2.3
考点:本试题主要考查了函数的奇偶性、对称性(中心对称的证明)及函数图象在解题中的运用,要求考生熟练掌握函数的性质,并能灵活运用性质求解.
点评:解决该试题的关键是熟练的运用函数的奇偶性和对称性来分析和解决问题,另外对于绝对值问题,常常去掉绝对值来分析得到结论。


科目:高中数学 来源: 题型:填空题
具有相同定义域D的函数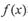 和,
和,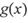 ,若对任意的
,若对任意的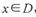 ,都有
,都有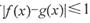 ,则称
,则称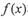 和
和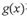 在D上是“密切函数”.给出定义域均为
在D上是“密切函数”.给出定义域均为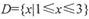 的四组函数:、
的四组函数:、
①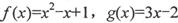
②
③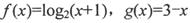
④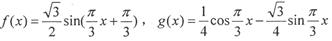
其中,函数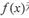 与
与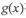 在D上为“密切函数”的是_______.
在D上为“密切函数”的是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知曲线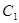 的方程是
的方程是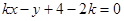
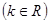 ,曲线
,曲线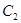 的方程是
的方程是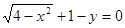 ,给出下列结论:
,给出下列结论:
①曲线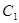 恒过定点
恒过定点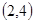 ;
;  ②曲线
②曲线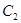 的图形是一个圆;
的图形是一个圆;
③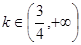 时,
时,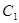 与
与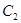 有一个公共点; ④若
有一个公共点; ④若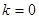 时,则
时,则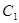 与
与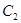 必无公共点。
必无公共点。
其中正确结论的序号是_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com