
已函数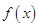 是定义在
是定义在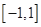 上的奇函数,在
上的奇函数,在 上时
上时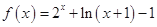
(Ⅰ)求函数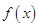 的解析式;
的解析式;
(Ⅱ)解不等式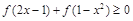 .
.
(Ⅰ) ;(Ⅱ)[0,1]
;(Ⅱ)[0,1]
【解析】
试题分析:(Ⅰ)由奇函数及在[0,1]上的解析式可得函数在[-1,0]上的解析式.从而即可得在[-1,1]上的解析式.本小题主要是考查分段函数的解析式问题.
(Ⅱ)由题意可知函数f(x)在[-1,1]上是递增函数.又因为函数f(x)是奇函数.所以通过 可得.
可得. 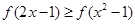 所以可得
所以可得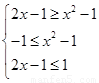 .从而可解得结论.本小题关键是通过函数的单调递增把函数值的大小转化为自变量的大小比较.
.从而可解得结论.本小题关键是通过函数的单调递增把函数值的大小转化为自变量的大小比较.
试题解析:(Ⅰ)设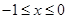 .则
.则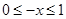 .所以
.所以 .又f(x)是奇函数.所以f(-x)=-f(x).f(x)=-f(-x)=
.又f(x)是奇函数.所以f(-x)=-f(x).f(x)=-f(-x)=
 .所以
.所以 .
.
(Ⅱ)易知f(x)是[-1,1]上增函数.由已知得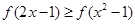 .等价于
.等价于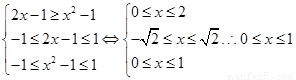 .所以不等式的解集为[0,1].
.所以不等式的解集为[0,1].
考点:1.分段函数.2.函数的单调性.3.函数的奇偶性.


科目:高中数学 来源:2014届湖北孝感高中高三年级九月调研考试理科数学试卷(解析版) 题型:解答题
已函数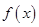 是定义在
是定义在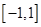 上的奇函数,在
上的奇函数,在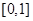 上
上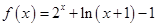 .
.
(1)求函数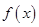 的解析式;并判断
的解析式;并判断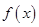 在
在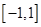 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省第13次月考) 题型:解答题
已知函数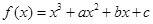 是定义在
是定义在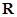 上的奇函数,其图象过点
上的奇函数,其图象过点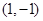 和
和
点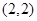 .
.
(Ⅰ)求函数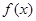 的解析式,并求
的解析式,并求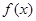 的单调区间;
的单调区间;
(Ⅱ)设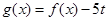 ,当实数
,当实数 如何取值时,关于
如何取值时,关于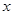 的方程
的方程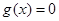 有且只有一个实
有且只有一个实
数根?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com