
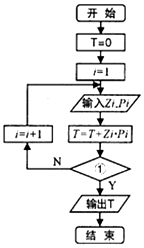
 某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率| 组别(i) | 睡眠时间 | 组中值(Zi) | 频数 | 频率(Pi) |
| 1 | [4.5,5.5) | 5 | 2 | 0.04 |
| 2 | [5.5,6.5) | 6 | 6 | 0.12 |
| 3 | [6.5,7.5) | 7 | 20 | 0.40 |
| 4 | [7.5,8.5) | 8 | 18 | 0.36 |
| 5 | [8.5,9.5) | 9 | 3 | 0.06 |
| 6 | [9.5,10.5) | 10 | 1 | 0.02 |
分析 (1)根据所给数据,结合众数、中位数的概念,求出数值即可;
(2)根据题目中算法流程图,共执行6次循环,得判断框①中应填入的条件;
(3)利用列举法求出基本事件数,计算对应的概率值.
解答 解:(1)根据所给数据,知众数是出现次数最多的数,为[6.5,7.5)的组中值7;
中位数两边频率相等,不妨设为x,
则0.04+0.12+(x-6.5)×0.4=0.5,
x=7.35;
(2)根据题目中算法流程图,用计算机统计平均睡眠时间,
总共执行6次循环,则判断框①中应填入的条件是
i≥6(或i=6或i>5);
(3)设第1组2个同学的睡眠时间为A、B,第5组3个同学的睡眠时间为c、d、e,
则从第1组和第5组中随机取出2个数据,包含的基本事件有
AB、Ac、Ad、Ae、Bc、Bd、Be、cd、ce、de共10个,
其中满足时间差的绝对值大于1小时的基本事件有
Ac、Ad、Ae、Bc、Bd、Be共6个,
故所求的概率为P=$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题考查了程序框图与频率分布表的应用问题,也考查了用列举法求古典概型的概率问题,是综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=|2x-1| | B. | f(x)=ex | C. | f(x)=x2+x+1 | D. | f(x)=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{7}{5}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com