
【题目】函数f(x)=ax3+bx2+cx+d的图象如图,则函数y=ax2+ ![]() bx+
bx+ ![]() 的单调递增区间是( )
的单调递增区间是( ) 
A.(﹣∞,2]
B.![]() ,+∞)
,+∞)
C.[﹣2,3]
D.![]() ,+∞)
,+∞)
【答案】D
【解析】解:不妨取a=1,
∵f(x)=x3+bx2+cx,∴f'(x)=3x2+2bx+c
由图可知f'(﹣2)=0,f'(3)=0
∴12﹣4b+c=0,27+6b+c=0,∴b=﹣1.5,c=﹣18
∴y=x2﹣ ![]() x﹣6,y'=2x﹣
x﹣6,y'=2x﹣ ![]() ,当x>
,当x> ![]() 时,y'>0
时,y'>0
∴y=x2﹣x﹣6的单调递增区间为:[ ![]() ,+∞)
,+∞)
故选D.
【考点精析】关于本题考查的二次函数的性质和利用导数研究函数的单调性,需要了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
上递减;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“正多边形都相似”的逆命题;
③“若m>0,则x2+x﹣m=0有实根”的逆否命题;
④“若x﹣ ![]() 是有理数,则x是无理数”的逆否命题.
是有理数,则x是无理数”的逆否命题.
A.①②③④
B.①③④
C.②③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数f(x)对于其定义域内的某一数x0 , 有 f(x0)=x0 , 则称x0是f (x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b﹣1 (a≠0).
(1)当a=1,b=﹣2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A,B的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+ ![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,a2=4,a4+a7=15.
(1)求数列{an}的通项公式;
(2)设bn=2 ![]() +n,求b1+b2+b3+…+b10的值.
+n,求b1+b2+b3+…+b10的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=﹣4x. (Ⅰ)已知点M在抛物线C上,它与焦点的距离等于5,求点M的坐标;
(Ⅱ)直线l过定点P(1,2),斜率为k,当k为何值时,直线l与抛物线:只有一个公共点;两个公共点;没有公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2, ![]()
![]() =0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A﹣PB﹣E的大小为( )
=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A﹣PB﹣E的大小为( ) 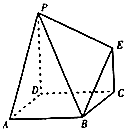
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com