
(本小题12分)离心率为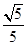 的椭圆
的椭圆 :
: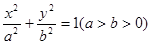 的左、右焦点分别为
的左、右焦点分别为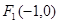 、
、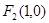 ,
,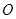 是坐标原点.
是坐标原点.
(1)求椭圆 的方程;
的方程;
(2)若直线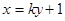 与
与 交于相异两点
交于相异两点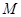 、
、 ,且
,且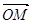

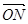
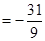 ,求
,求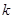 .(其中
.(其中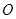 是坐标原点)
是坐标原点)
科目:高中数学 来源: 题型:
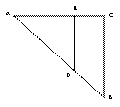
(本小题12分)如图为等腰直角三角形直角边长为8,![]() ,
,![]() ,沿DE将三角形ADE折起使得点A在平面BCED上的射影是点C, MC=
,沿DE将三角形ADE折起使得点A在平面BCED上的射影是点C, MC=![]() AC.
AC.
(Ⅰ)在BD上确定点N的位置,使得![]() ;
;
 (Ⅱ)求CN与平面ABD所成角的正弦值.
(Ⅱ)求CN与平面ABD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2011年云南省建水一中高一上学期期中考试数学 题型:解答题
(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产W和R型两种产品。经市场预测,生产W型产品所获利润 (万元)与投入资金
(万元)与投入资金 (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元。生产R型产品所获利润
万元。生产R型产品所获利润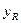 (万元)与投入资金
(万元)与投入资金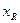 (
( 万元)满足关系
万元)满足关系 ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产W和R型两种产品。经市场预测,生产W型产品所获利润![]() (万元)与投入资金
(万元)与投入资金![]() (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5万元。生产R型产品所获利润
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5万元。生产R型产品所获利润![]() (万元)与投入资金
(万元)与投入资金![]() (万元)满足关系
(万元)满足关系![]() ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com