
分析 (1)将f(x)的解析式整理可得f(x)=2+$\frac{1}{x-2}$,由g(x)的图象先向右平移2个单位,再向上平移2个单位得到.
再由g(x)的对称中心,即可得到所求f(x)的对称中心;
(2)若ab+1≠0,则f(x)不为常函数.设f(x)的图象上任一点为(m,n),证明点(n,m)也在f(x)的图象上,即可得证.
解答 解:(1)若a=$\frac{1}{2}$,b=-$\frac{3}{2}$,即有f(x)=$\frac{x-\frac{3}{2}}{\frac{1}{2}x-1}$
=$\frac{2x-3}{x-2}$=2+$\frac{1}{x-2}$,
则f(x)的图象可由g(x)=$\frac{1}{x}$的图象先向右平移2个单位,
再向上平移2个单位得到.
由g(x)的图象的对称中心为(0,0),则f(x)的图象对称中心为(2,2);
(2)证明:若ab+1≠0,则f(x)不为常函数.
设f(x)的图象上任一点为(m,n),
即有f(m)=n,即为$\frac{m+b}{am-1}$=n,
即有m+b=amn-n,
可得(an-1)m=n+b,
即有m=$\frac{an-1}{n+b}$,则f(n)=m,
即点(n,m)也在函数f(x)的图象上,
而(m,n)和(n,m)关于直线y=x对称.
故f(x)的图象必关于直线y=x对称.
点评 本题考查函数的图象变换和函数的对称中心的求法,考查函数的对称性的证明,注意运用点的对称,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,$\frac{\sqrt{2}}{2}$) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:5 | B. | 1:4 | C. | 1:3 | D. | 1:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
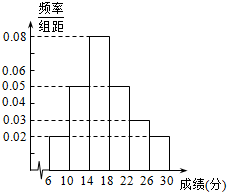 为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com