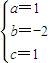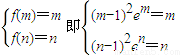【答案】
分析:(Ⅰ)求导函数,根据函数f(x)=(ax
2+bx+c)e
x在x=1处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为-1,建立方程组,从而可得f(x)的解析式为f(x)=(x
2-2x+1)e
x.
(Ⅱ)由(Ⅰ)得f'(x)=(x
2-1)e
x,假设当x>1时,f(x)存在“保值区间”[m,n](n>m>1),进而问题转化为(x-1)
2e
x-x=0有两个大于1的不等实根,构造新函数h(x)=(x-1)
2e
x-x(x≥1),可判断存在唯一x
∈(1,2),使得h′(x
)=0,h(x)在(1,x
)上单调递减,在(x
,+∞)上单调递增,从而可得当x>1时,h(x)的图象与x轴有且只有一个交点,即方程(x-1)
2e
x-x=0有且只有一个大于1的根,与假设矛盾,故可得证.
解答:解:(Ⅰ)∵f(x)=(ax
2+bx+c)e
x,
∴f′(x)=[ax
2+(2a-b)x+(b+c)]e
x,(2分)
∵函数f(x)=(ax
2+bx+c)e
x在x=1处取得极小值,其图象过点A(0,1),且在点A处切线的斜率为-1.
∴
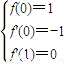
,即
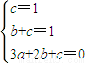
,解得
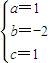
所以f(x)的解析式为f(x)=(x
2-2x+1)e
x.(4分)
(Ⅱ)由(Ⅰ)得f'(x)=(x
2-1)e
x,
假设当x>1时,f(x)存在“保值区间”[m,n](n>m>1)
因为当x>1时,f'(x)=(x
2-1)e
x>0,所以f(x)在区间(1,+∞)上是增函数
∴
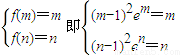
于是问题转化为(x-1)
2e
x-x=0有两个大于1的不等实根. (6分)
现在考查函数h(x)=(x-1)
2e
x-x(x≥1),h′(x)=(x
2-1)e
x-1
令φ(x)=(x
2-1)e
x-1,∴φ′(x)=(x
2+2x-1)e
x,
当x>1时,φ′(x)>0
∴φ(x)在(1,+∞)上是增函数,即h′(x)在(1,+∞)上是增函数
∴h′(1)=-1<0,,h′(2)=3e
2-1>0
∴存在唯一x
∈(1,2),使得h′(x
)=0(10分)
当x变化时,h′(x),h(x)的变化情况如下表:
| x | (1,x) | x | (x,+∞) |
| h′(x) | - | | + |
| h(x) | 单调递减 | 极小值 | 单调递增 |
所以,h(x)在(1,x
)上单调递减,在(x
,+∞)上单调递增.
∴h(x
)<h(1)=-1<0
∵h(2)=e
2-2>0
∴当x>1时,h(x)的图象与x轴有且只有一个交点
即方程(x-1)
2e
x-x=0有且只有一个大于1的根,与假设矛盾
故当x>1时,f(x)不存在“保值区间”.(13分)
点评:本题以函数的性质为载体,考查导数知识的运用,考查函数的解析式,考查新定义,同时考查反证法思想的运用,综合性强.

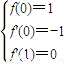 ,即
,即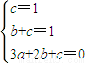 ,解得
,解得