
分析 (1)由两角和的正弦公式、二倍角的正弦公式化简解析式,由正弦函数的增区间求出f(x)的增区间;
(2)由(1)化简f(α)=$\frac{3\sqrt{2}}{8}$,由角之间的关系、诱导公式、二倍角余弦公式的变形求出sin4α的值.
解答 解:(1)由题意得f(x)=sin(x+$\frac{π}{4}$)cosx
=$\frac{\sqrt{2}}{2}(sinxcosx+co{s}^{2}x)$=$\frac{\sqrt{2}}{4}(sin2x+cos2x+1)$
=$\frac{1}{2}sin(2x+\frac{π}{4})+\frac{\sqrt{2}}{4}$,
由$2kπ-\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}(k∈Z)$得,
$kπ-\frac{3π}{8}≤x≤kπ+\frac{π}{8}(k∈Z)$,
∴函数f(x)的单调递增区间是$[kπ-\frac{3π}{8},kπ+\frac{π}{8}](k∈Z)$;
(2)由(1)得,f(α)=$\frac{1}{2}sin(2α+\frac{π}{4})+\frac{\sqrt{2}}{4}$=$\frac{3\sqrt{2}}{8}$,
∴$sin(2α+\frac{π}{4})=\frac{\sqrt{2}}{4}$,
∴$sin4α=-cos(4α+\frac{π}{2})$=-[1-$2si{n}^{2}(2α+\frac{π}{4})$]
=$-\frac{3}{4}$.
点评 本题考查正弦函数的性质,两角和的正弦公式、二倍角的正弦公式,以及诱导公式、二倍角余弦公式的变形,其中变角是解题的关键,考查化简、变形能力.


科目:高中数学 来源: 题型:解答题
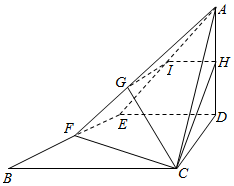 △ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点.
△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{9}{4}$,+∞) | B. | [2,+∞) | C. | (-∞,$\frac{9}{4}$] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 2$\sqrt{2}$-3 | C. | 2$\sqrt{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,$\frac{4}{3}$ | B. | 3,$\frac{3}{2}$ | C. | 4,$\frac{4}{3}$ | D. | 4,$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 80-$\frac{20}{3}$π | B. | 80+$\frac{20}{3}$π | C. | 112+(2$\sqrt{29}$-4)π | D. | 112+2$\sqrt{29}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com