
 )2
)2 

 与g(t)=t+1(t≠1)
与g(t)=t+1(t≠1) 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:北京模拟题 题型:解答题
 ,P1(2,3),求证:点Pn(xn,yn)(n∈N*)存在一个半径为
,P1(2,3),求证:点Pn(xn,yn)(n∈N*)存在一个半径为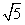 的收敛圆。
的收敛圆。 查看答案和解析>>
科目:高中数学 来源:福建省月考题 题型:单选题
 )=﹣f(x)的函数,我们称为满足“倒负”变换的函数数,下列函数
)=﹣f(x)的函数,我们称为满足“倒负”变换的函数数,下列函数 ②y=x+
②y=x+ ③y=
③y= 中满足“倒负”变换的函数是
中满足“倒负”变换的函数是查看答案和解析>>
科目:高中数学 来源:浙江省模拟题 题型:单选题
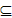 D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有
D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有 查看答案和解析>>
科目:高中数学 来源:专项题 题型:单选题
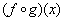 和(f·g)(x);对任意x∈R,
和(f·g)(x);对任意x∈R,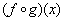 =f(g(x));(f·g)(x)=f(x)g(x),则下列恒等式成立的是
=f(g(x));(f·g)(x)=f(x)g(x),则下列恒等式成立的是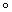 g)·h)(x)=((f·h)
g)·h)(x)=((f·h)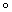 (g·h))(x)
(g·h))(x) 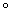 h)(x)=((f
h)(x)=((f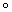 h)·(g
h)·(g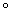 h))(x)
h))(x) 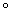 g)
g)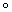 h)(x)=((f
h)(x)=((f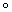 h)
h)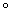 (g
(g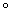 h))(x)
h))(x) 查看答案和解析>>
科目:高中数学 来源:同步题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com