
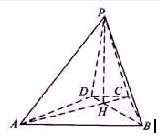
如图,已知四棱锥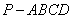 的底面为等腰梯形,
的底面为等腰梯形,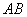 ∥
∥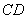 ,
,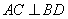 ,垂足为
,垂足为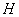 ,
, 是四棱锥的高。
是四棱锥的高。
(Ⅰ)证明:平面
 平面
平面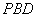 ;
;
(Ⅱ)若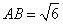 ,
,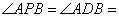 60°,求四棱锥
60°,求四棱锥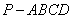 的体积。
的体积。
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分。作答时用2B铅笔在答题卡上把所选题目的题号涂黑。
[番茄花园1]1.
 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com