

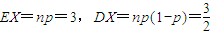 ,
,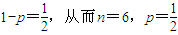
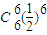 +
+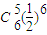 +
+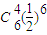 +
+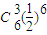
 =
=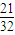


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 环数 | 7 | 8 | 9 | 10 |
| 命中次数 | 2 | 7 | 8 | 3 |
查看答案和解析>>
科目:高中数学 来源:2010年北京市朝阳区高三第二次模拟考试数学(理) 题型:解答题
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 | 7 | 8 | 9 | 10 |
| 命中次数 | 2 | 7 | 8 | 3 |
 次、
次、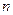 次,每个基本事件为(m,n).
次,每个基本事件为(m,n). ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省六校联合体高三第二次联考数学文卷 题型:解答题
(本题满分14分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
|
环数 |
7 |
8 |
9 |
10 |
|
命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为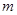 次、
次、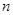 次,每个基本事件为(m,n).求“
次,每个基本事件为(m,n).求“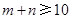 ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com