|
|
|
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.
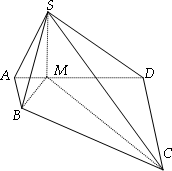
(Ⅰ)证明:BM⊥平面SMC;
(Ⅱ)设三棱锥C-SBM与四棱锥S-ABCD的体积分别为V1与V,求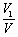 的值. 的值.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△ABC中,B=120°,AC=7,AB=5,则△ABC的面积为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)=loga(x3-ax)>0且a≠1)在区间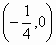 内单调递增,则实数a的取值范围是 内单调递增,则实数a的取值范围是
|
| [ ] |
A. |
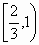
|
B. |
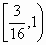
|
C. |
[ ,1)∪(1,3] ,1)∪(1,3]
|
D. |
(1,3]
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若空间三条直线a、b、c满足a⊥b,b∥c,则直线a与c
|
| [ ] |
A. |
一定平行
|
B. |
一定相交
|
C. |
一定是异面直线
|
D. |
一定垂直
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
平面向量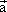 与 与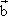 的夹角为60°, 的夹角为60°,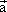 =(2,0),| =(2,0),|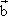 |=1,则| |=1,则|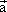 +2 +2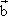 |= |=
|
| [ ] |
A. |
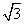
|
B. |
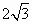
|
C. |
4
|
D. |
12
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知点P为双曲线 - -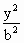 =1(a>0,b>0)的右支上一点F1、F2为双曲线的左、右焦点,使( =1(a>0,b>0)的右支上一点F1、F2为双曲线的左、右焦点,使(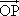 + +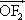 )· )·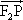 =0(O为坐标原点),且|PF1|= =0(O为坐标原点),且|PF1|=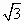 |PF2|,则双曲线离心率为 |PF2|,则双曲线离心率为
|
| [ ] |
A. |
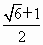
|
B. |
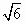 +1 +1
|
C. |
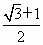
|
D. |
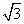 +1 +1
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
现有8名青年,其中5名能任英语翻译工作,4名能胜任电脑软件设计工作,且每人至少能胜这两项工作中的一项,现从中选5人,承担一项任务,其中3人从事英语翻译工作,2人从事软件设计工作,则不同的选派方法有
|
| [ ] |
A. |
60种
|
B. |
54种
|
C. |
30种
|
D. |
42种
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设复数z满足z(1+2i)=4-2i(i为虚数单位),则|z|=
|
| [ ] |
A. |
l
|
B. |
2
|
C. |
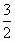
|
D. |
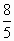
|
|
|
查看答案和解析>>

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案