已知点A(4,3)和圆C:(x-2)2+y2=4
(1)求圆C关于点A对称的圆C1的标准方程;
(2)求过点A并且与圆C相切的直线方程.
【答案】
分析:(1)由题意可设,圆C关于点A对称的圆C
1的标准方程为(x-a)
2+(y-b)
2=4则可得,(2,0)与(a,b)关于A(4,3)对称,可求a,b
(2)设所求的切线方程为y-3=k(x-4),然后根据直线与圆相切的 性质,可知圆心(2,0)到直线kx-y+3-4k=0的距离d=2可求k,进而可求切线方程
解答:解:(1)由题意可设,圆C关于点A对称的圆C
1的标准方程为(x-a)
2+(y-b)
2=4
则可得,(2,0)与(a,b)关于A(4,3)对称
则
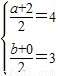
,解可得,a=6,b=6,所求的圆的方程为(x-6)
2+(y-6)
2=4
(2)设所求的切线方程为y-3=k(x-4)即kx-y+3-4k=0
由直线与圆相切的 性质,可知圆心(2,0)到直线kx-y+3-4k=0的距离d=

解可得,k=
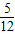
即直线方程为5x-12y+16=0
而当直线为x=4时也与圆相切,
综上可得,所求的切线方程为5x-12y+16=0或x=4
点评:本题主要考查了两点关于点对称 性质的应用及直线与圆相切性质的应用,解(2)是一定要 注意有两条切线

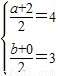 ,解可得,a=6,b=6,所求的圆的方程为(x-6)2+(y-6)2=4
,解可得,a=6,b=6,所求的圆的方程为(x-6)2+(y-6)2=4
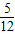 即直线方程为5x-12y+16=0
即直线方程为5x-12y+16=0

 名校课堂系列答案
名校课堂系列答案