
 的△ABC中,角A、B、C所对应的边为a,b,c成等差数列,B=30°.
的△ABC中,角A、B、C所对应的边为a,b,c成等差数列,B=30°. ,可得
,可得  •ac•sinB=
•ac•sinB= ,解得 ac=6.
,解得 ac=6.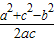 =
=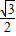 ③.
③.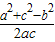 =
=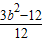 =
=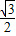 ,解得 b=1+
,解得 b=1+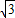 ,
,

科目:高中数学 来源:2012年浙江省台州市高考数学一模试卷(理科)(解析版) 题型:解答题
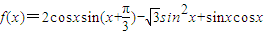 .
.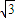 的△ABC中,若角A为锐角,f(A)=0,求A所对的边的取值范围.
的△ABC中,若角A为锐角,f(A)=0,求A所对的边的取值范围.查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下学期期末数学试卷(解析版) 题型:解答题
(14分)在面积为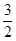 的△ABC中,角A、B、C所对应的边为
的△ABC中,角A、B、C所对应的边为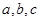 成等差数列,
成等差数列,
B=30°.
(1)求 ;(2)求边
;(2)求边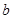 。
。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省厦门六中高二(上)10月月考数学试卷(解析版) 题型:解答题
 的△ABC中,角A、B、C所对应的边为a,b,c成等差数列,B=30°.
的△ABC中,角A、B、C所对应的边为a,b,c成等差数列,B=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com