
已知抛物线 (
( 且
且 为常数),
为常数), 为其焦点.
为其焦点.

(1)写出焦点 的坐标;
的坐标;
(2)过点 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 ,求直线
,求直线 的斜率;
的斜率;
(3)若线段 是过抛物线焦点
是过抛物线焦点 的两条动弦,且满足
的两条动弦,且满足 ,如图所示.求四边形
,如图所示.求四边形 面积的最小值
面积的最小值 .
.
(1)(a,0);(2)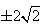 ; (3)
; (3) 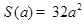 .
.
【解析】
试题分析:(1)∵抛物线方程为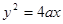 (a>0),∴焦点为F(a,0).
(a>0),∴焦点为F(a,0).
(2)设满足题意的点为P(x0,y0)、Q(x1,y1).
∵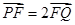 ,
,
∴(a-x0,-y0)=2(x1-a,y1),即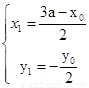 .
.
又y12=4ax1,y02=4ax0,
∴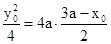 ,进而可得x0=2a,
,进而可得x0=2a,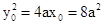 ,即y0=±2
,即y0=±2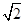 a.
a.
∴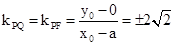 .
.
(3) 由题意可知,直线AC不平行于x轴、y轴(否则,直线AC、BD与抛物线不会有四个交点)。
于是,设直线AC的斜率为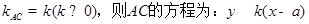 . 12分
. 12分
联立方程组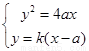 ,化简得
,化简得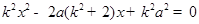 (设点
(设点 ),则
),则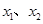 是此方程的两个根.
是此方程的两个根.
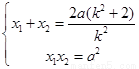 .
13分
.
13分
弦长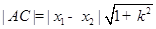
=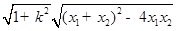
=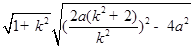
=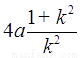 .
15分
.
15分
又 ,
,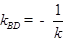 .
.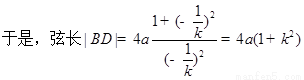 . 16分
. 16分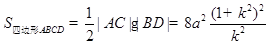
=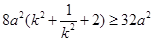 ,当且仅当
,当且仅当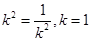 时,四边形
时,四边形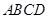 面积的最小值
面积的最小值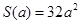 .18分
.18分
考点:直线与抛物线的位置关系,平面向量的坐标运算。
点评:中档题,涉及曲线的位置关系问题,往往通过联立方程组,消元后,应用韦达定理,简化运算过程。本题(2)通过应用平面向量共线的条件,利用“代入法”,得到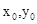 的关系,进一步求得直线的斜率。(3)利用函数的观点及均值定理,确定得到面积的最小值。应用均值定理要注意“一正,二定,三相等”,缺一不可。
的关系,进一步求得直线的斜率。(3)利用函数的观点及均值定理,确定得到面积的最小值。应用均值定理要注意“一正,二定,三相等”,缺一不可。


科目:高中数学 来源: 题型:
 如图,已知抛物线的方程为x2=2px(p>0,为常数),过点M(0,m)且倾斜角为θ(0<θ<
如图,已知抛物线的方程为x2=2px(p>0,为常数),过点M(0,m)且倾斜角为θ(0<θ<| π |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分8分,第3小题满分7分.
已知抛物线![]() (
(![]() 且
且![]() 为常数),
为常数),![]() 为其焦点.
为其焦点.
(1)写出焦点![]() 的坐标;
的坐标;
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
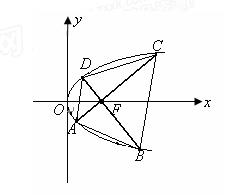
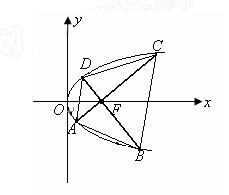
(3)若线段![]() 是过抛物线焦点
是过抛物线焦点![]() 的两条动弦,且满足
的两条动弦,且满足![]() ,如图所示.求四边形
,如图所示.求四边形![]() 面积的最小值
面积的最小值![]() .
.
查看答案和解析>>
科目:高中数学 来源:上海市嘉定、黄浦区2010届高三第二次模拟考试数学文 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分8分,第3小题满分7分.
已知抛物线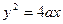 (
(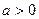 且
且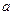 为常数),
为常数),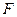 为其焦点.
为其焦点.
(1)写出焦点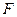 的坐标;
的坐标;
(2)过点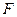 的直线与抛物线相交于
的直线与抛物线相交于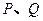 两点,且
两点,且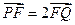 ,求直线
,求直线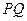 的斜率;
的斜率;
(3)若线段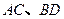 是过抛物线焦点
是过抛物线焦点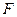 的两条动弦,且满足
的两条动弦,且满足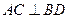 ,如图所示.求四边形
,如图所示.求四边形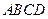 面积的最小值
面积的最小值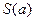 .
.
查看答案和解析>>
科目:高中数学 来源:上海市嘉定、黄浦区2010届高三第二次模拟考试数学文 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分8分,第3小题满分7分.
已知抛物线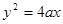 (
(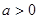 且
且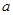 为常数),
为常数), 为其焦点.
为其焦点.
(1)写出焦点 的坐标;
的坐标;
(2)过点 的直线与抛物线相交于
的直线与抛物线相交于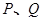 两点,且
两点,且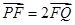 ,求直线
,求直线 的斜率;
的斜率;
(3)若线段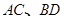 是过抛物线焦点
是过抛物线焦点 的两条动弦,且满足
的两条动弦,且满足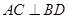 ,如图所示.求四边形
,如图所示.求四边形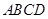 面积的最小值
面积的最小值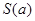 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com