解:(1)由题意,可知:c=1且a+c=

+1,
∴a=

,可得b
2=a
2-c
2=1
因此,椭圆C的方程为:

+y
2=1
(2)设直线l的方程为:y=k(x-1)
直线交椭圆C于A(x
1,y
1),B(x
2,y
2),
由
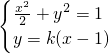
消去y,得(1+2k
2)x
2-4k
2x+2k
2-2=0,
由根与系数的关系,得

∵M(

,0),可得
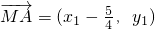
,
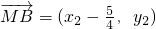
∴

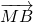
=(x
1-

)(x
2-

)+y
1y
2=-

(x
1+x
2)+x
1x
2+

+y
1y
2,
∵y
1=k(x
1-1),y
2=k(x
2-1)
∴

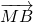
=-

(x
1+x
2)+x
1x
2+

+y
1y
2
=-

(x
1+x
2)+x
1x
2+

+k
2(x
1-1)(x
2-1)
=-

•
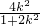
+
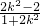
+

+k
2(
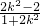
-
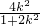
+1)=-

∴对于任意的k∈R,

=-

(定值).
分析:(1)根据题意,可得c=1且a=

,再用平方关系算出b
2=1,从而得到椭圆C的方程.
(2)设直线交椭圆C于A(x
1,y
1),B(x
2,y
2),将直线l的方程y=k(x-1)与椭圆C联解消去y,得关于x的方程,再运用根与系数关系算出x
1+x
2、x
1x
2关于k的式子,最后利用向量数量积的坐标公式将

化简整理,即可得到对于任意的k∈R,

=-

(定值).
点评:本题给出椭圆方程,求解过焦点的直线与椭圆相交所得向量数量积的问题,着重考查了椭圆的几何性质和直线与椭圆位置关系等知识,属于中档题.

 的左、右焦点,点P为椭圆上任意一点,P到焦点F2(1,0)的距离的最大值为
的左、右焦点,点P为椭圆上任意一点,P到焦点F2(1,0)的距离的最大值为 +1.
+1. ,0),过点F2且斜率为k的直线l与椭圆C相交于A,B两点.对于任意的k∈R,
,0),过点F2且斜率为k的直线l与椭圆C相交于A,B两点.对于任意的k∈R, 是否为定值?若是求出这个定值;若不是说明理由.
是否为定值?若是求出这个定值;若不是说明理由. +1,
+1, ,可得b2=a2-c2=1
,可得b2=a2-c2=1 +y2=1
+y2=1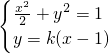 消去y,得(1+2k2)x2-4k2x+2k2-2=0,
消去y,得(1+2k2)x2-4k2x+2k2-2=0,
 ,0),可得
,0),可得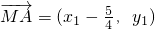 ,
,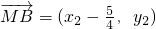

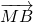 =(x1-
=(x1- )(x2-
)(x2- )+y1y2=-
)+y1y2=- (x1+x2)+x1x2+
(x1+x2)+x1x2+ +y1y2,
+y1y2,
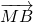 =-
=- (x1+x2)+x1x2+
(x1+x2)+x1x2+ +y1y2
+y1y2 (x1+x2)+x1x2+
(x1+x2)+x1x2+ +k2(x1-1)(x2-1)
+k2(x1-1)(x2-1) •
•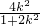 +
+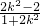 +
+ +k2(
+k2(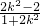 -
-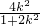 +1)=-
+1)=-
 =-
=- (定值).
(定值). ,再用平方关系算出b2=1,从而得到椭圆C的方程.
,再用平方关系算出b2=1,从而得到椭圆C的方程. 化简整理,即可得到对于任意的k∈R,
化简整理,即可得到对于任意的k∈R, =-
=- (定值).
(定值).

 (a>b>0)的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为
(a>b>0)的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为 +1,且△PF1F2的最大面积为1。
+1,且△PF1F2的最大面积为1。 ,过点F2且斜率为k的直线L与椭圆C相交于A,B两点。对于任意的k∈R,
,过点F2且斜率为k的直线L与椭圆C相交于A,B两点。对于任意的k∈R, 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。  的左右焦点,P是椭圆C上的一点,且
的左右焦点,P是椭圆C上的一点,且 的面积为
的面积为
 ,过点F2且斜率为k的直线l与椭圆C相交于A,B两点,对于任意的
,过点F2且斜率为k的直线l与椭圆C相交于A,B两点,对于任意的 是否为定值?若是求出这个定值;若不是说明理由.
是否为定值?若是求出这个定值;若不是说明理由.