如图，正方形ABCD的边长为3，E为DC的中点，AE与BD相交于F，则
的值是（ ）
A．
B．
C．
D．
科目：高中数学 来源：2013-2014学年甘肃省张掖市高三第三次诊断考试文科数学试卷（解析版） 题型：解答题
随着工业化以及城市车辆的增加，城市的空气污染越来越严重，空气质量指数API一直居高不下，对人体的呼吸系统造成了严重的影响．现调查了某市500名居民的工作场所和呼吸系统健康，得到
列联表如下：
| 室外工作 | 室内工作 | 合计 |
有呼吸系统疾病 | 150 |
|
|
无呼吸系统疾病 |
| 100 |
|
合计 | 200 |
|
|
（1）补全列联表；
（2）你是否有95%的把握认为感染呼吸系统疾病与工作场所有关；
（3）现采用分层抽样从室内工作的居民中抽取一个容量为6的样本，将该样本看成一个总体，从中随机的抽取两人，求两人都有呼吸系统疾病的概率．
参考公式与临界值表：K2＝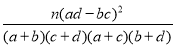
P(K2≥k0) | 0．100 | 0．050 | 0．025 | 0．010 | 0．001 |
k0 | 2．706 | 3．841 | 5．024 | 6．635 | 10．828 |
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖南省长沙市高考二模理科数学试卷（解析版） 题型：解答题
某地一渔场的水质受到了污染．渔场的工作人员对水质检测后，决定往水中投放一种药剂来净化水质. 已知每投放质量为
个单位的药剂后，经过x天该药剂在水中释放的浓度y（毫克/升）满足y=mf(x)，其中
，当药剂在水中释放的浓度不低于6（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于6（毫克/升）且不高于18（毫克/升）时称为最佳净化.
（1）如果投放的药剂质量为m=6，试问渔场的水质达到有效净化一共可持续几天?
（2）如果投放的药剂质量为m，为了使在8天（从投放药剂算起包括第8天）之内的渔场的水质达到最佳净化，试确定应该投放的药剂质量m的取值范围.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖南省长沙市高考二模理科数学试卷（解析版） 题型：填空题
已知直角坐标系xOy中，直线l的参数方程为
. 以直角坐标系xOy中的原点O为极点，x轴的非负半轴为极轴，圆C的极坐标方程为
，则圆心C到直线l距离为______.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖南省益阳市高三模拟考试理科数学试卷（解析版） 题型：解答题
已知函数
，
．
（1）若直线
恰好为曲线
的切线时，求实数
的值；
（2）当
，
时（其中无理数
），
恒成立，试确定实数的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，故
，即
，所以
．
，设
，若
，则
的取值范围是____．
的展开式中常数项为（ ）
时，求
的值； 
在
上的值域.
为虚数单位，则
等于（ ）
B．
C．
D．