
某地一渔场的水质受到了污染.渔场的工作人员对水质检测后,决定往水中投放一种药剂来净化水质. 已知每投放质量为 个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中
个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中 ,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为m=6,试问渔场的水质达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,试确定应该投放的药剂质量m的取值范围.
(1)8天;(2)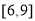
【解析】
试题分析:(1)由已知得,经过x天该药剂在水中释放的浓度 y=mf(x)是关于自变量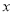 的分段函数,渔场的水质达到有效净化,只需
的分段函数,渔场的水质达到有效净化,只需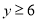 ,当m=6时,
,当m=6时,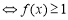 ,相当于知道函数值的取值范围,求自变量
,相当于知道函数值的取值范围,求自变量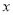 的取值范围,即可持续的天数确定;(2)由题意知,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,只需在这8天内的每一天均有
的取值范围,即可持续的天数确定;(2)由题意知,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,只需在这8天内的每一天均有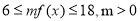 恒成立即可,转化为求分段函数求值域问题,使其含于
恒成立即可,转化为求分段函数求值域问题,使其含于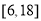 即可.
即可.
(1)由题设:投放的药剂质量为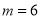 ,渔场的水质达到有效净化
,渔场的水质达到有效净化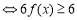
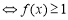
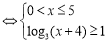 或
或
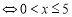 或
或 ,即:
,即: ,
,
所以如果投放的药剂质量为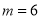 ,自来水达到有效净化一共可持续8天 . 6分
,自来水达到有效净化一共可持续8天 . 6分
(2)由题设: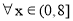 ,
,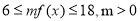 ,∵
,∵ ,
,
∴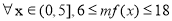 ,且
,且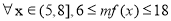 ,
,
∴ 且
且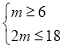 ,所以
,所以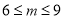 ,投放的药剂质量m的取值范围为
,投放的药剂质量m的取值范围为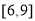 .
.
考点:分段函数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试理科数学试卷(解析版) 题型:选择题
已知 为执行如图所示的程序框图输出的结果,则二项式
为执行如图所示的程序框图输出的结果,则二项式 的展开式中含
的展开式中含 项的系数是( ).
项的系数是( ).

A.192 B.32 C.96 D.-192
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校联考第二次考试理科数学试卷(解析版) 题型:填空题
在直角坐标系 中,曲线
中,曲线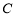 的参数方程为
的参数方程为 为参数),在以原点
为参数),在以原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .则
.则 与
与 的交点直角坐标为 .
的交点直角坐标为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校第二次联考文科数学试卷(解析版) 题型:选择题
已知 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,且
,且 ,
, ,
, ,对于数列
,对于数列 ,任取正整数
,任取正整数 ,则前k项和大于
,则前k项和大于 的概率是( )
的概率是( )
A. B.
B. C.
C. D.
D.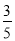
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校第二次联考文科数学试卷(解析版) 题型:选择题
“ ”是“x>l"的( )
”是“x>l"的( )
A.充要条件 B.必要非充分条件
C.充分非必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长为3,E为DC的中点,AE与BD相交于F,则 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com