
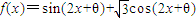 的图象关于原点对称,且满足对于
的图象关于原点对称,且满足对于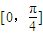 内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是( )
内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是( )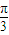
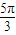
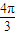
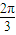
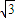 ,得θ=
,得θ=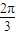 +kπ(k∈Z).再根据函数f(x)区间
+kπ(k∈Z).再根据函数f(x)区间 内恒有(x1-x2)[f(x1)-f(x2)]<0,得函数f(x)为减函数,利用辅助角公式并结合函数y=Asin(ωx+φ)的性质讨论f(x)的单调减区间,即可得到取k=0,得θ=
内恒有(x1-x2)[f(x1)-f(x2)]<0,得函数f(x)为减函数,利用辅助角公式并结合函数y=Asin(ωx+φ)的性质讨论f(x)的单调减区间,即可得到取k=0,得θ=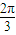 时满足题设的两个条件.
时满足题设的两个条件. 的图象关于原点对称,
的图象关于原点对称,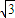 cosθ=0,
cosθ=0,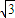 ,θ=
,θ=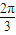 +kπ,k∈Z
+kπ,k∈Z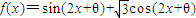 =2sin(2x+θ+
=2sin(2x+θ+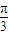 )
)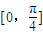 内恒有(x1-x2)[f(x1)-f(x2)]<0,即函数为减函数
内恒有(x1-x2)[f(x1)-f(x2)]<0,即函数为减函数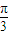 ≤2x+θ+
≤2x+θ+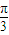 ≤θ+
≤θ+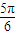 ,
,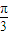 ,得集合M={t|θ+
,得集合M={t|θ+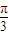 ≤t≤θ+
≤t≤θ+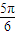 },且M?[
},且M?[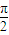 +2mπ,
+2mπ,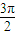 +2mπ],m∈Z.
+2mπ],m∈Z.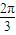 ,M=[π,
,M=[π,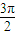 }满足题设的两个条件
}满足题设的两个条件

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)已知函数![]() ,若函数
,若函数![]() 的图象与函数
的图象与函数![]() 的图象关于原点对称.(1)写出函数
的图象关于原点对称.(1)写出函数![]() 的解析式; (2)求不等式
的解析式; (2)求不等式![]() 的解集
的解集![]() ; (3)问是否存在
; (3)问是否存在![]() ,使不等式
,使不等式![]() 的解集恰好是
的解集恰好是![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:安徽省2012届高二下学期期末联考数学(文 题型:填空题
对于函数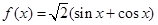 , 给出下列四个命题:
, 给出下列四个命题:
① 存在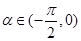 , 使
, 使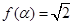 ;
;
② 存在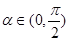 , 使
, 使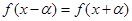 恒成立;
恒成立;
③ 存在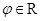 , 使函数
, 使函数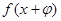 的图象关于坐标原点成中心对称;
的图象关于坐标原点成中心对称;
④ 函数f(x)的图象关于直线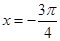 对称;
对称;
⑤ 函数f(x)的图象向左平移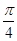 就能得到
就能得到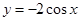 的图象
的图象
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
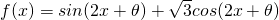 的图象关于原点对称,且满足对于
的图象关于原点对称,且满足对于 内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是
内任意两个数x1,x2,恒有(x1-x2)[f(x1)-f(x2)]<0的θ的一个取值可以是



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com