
(本题满分16分)甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润 (元)与年产量
(元)与年产量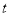 (吨)满足函数关系
(吨)满足函数关系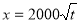 .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方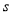 元(以下称
元(以下称 为赔付价格).
为赔付价格).
(Ⅰ)将乙方的年利润w (元)表示为年产量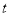 (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额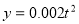 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格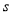 是多少?
是多少?
(Ⅰ) ,
,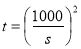 (Ⅱ)
(Ⅱ)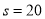
【解析】
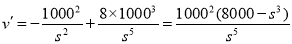 试题分析:(Ⅰ)解决利润问题,关键分清年利润与单位利润,收益与支出:乙方的实际年利润为乙方的年利润减去每年赔付甲方额:
试题分析:(Ⅰ)解决利润问题,关键分清年利润与单位利润,收益与支出:乙方的实际年利润为乙方的年利润减去每年赔付甲方额: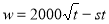
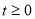 .这是关于
.这是关于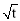 的二次函数,求其最值,须明确定义区间及对称轴之间关系:当
的二次函数,求其最值,须明确定义区间及对称轴之间关系:当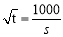 ,
,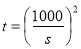 时,
时, 取得最大值;(Ⅱ)甲方净收入为乙方每年赔付甲方额减去每年受乙方生产影响的经济损失金额:甲方净收入为
取得最大值;(Ⅱ)甲方净收入为乙方每年赔付甲方额减去每年受乙方生产影响的经济损失金额:甲方净收入为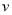 元,则
元,则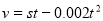 .
.
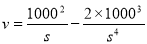 ,这需利用导数求其最值:
,这需利用导数求其最值:
令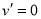 ,得
,得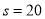 .当
.当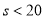 时,
时,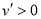 ;当
;当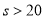 时,
时,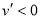 ,所以
,所以 时,
时,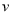 取得最大值.
取得最大值.
试题解析(Ⅰ)乙方的实际年利润为: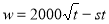
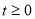 . (5分)
. (5分)
 ,
,
当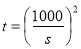 时,
时, 取得最大值.
取得最大值.
所以乙方取得最大年利润的年产量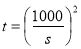 (吨).
(吨).
(Ⅱ)设甲方净收入为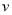 元,则
元,则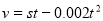 .
.
将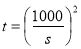 代入上式,得:
代入上式,得: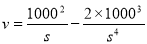 . (5分)
. (5分)
又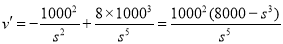
令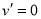 ,得
,得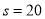 .
.
当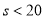 时,
时,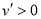 ;当
;当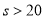 时,
时,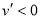 ,所以
,所以 时,
时,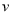 取得最大值.
取得最大值.
因此甲方向乙方要求赔付价格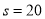 (元/吨)时,获最大净收入. (8分)
(元/吨)时,获最大净收入. (8分)
考点:利用导数求函数最值


科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三新高考单科综合调研三理科数学试卷(解析版) 题型:填空题
设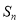 为数列
为数列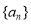 的前
的前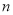 项和,若
项和,若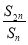
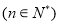 是非零常数,则称该数列为“和等比数列”;若数列
是非零常数,则称该数列为“和等比数列”;若数列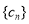 是首项为
是首项为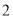 ,公差为
,公差为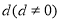 的等差数列,且数列
的等差数列,且数列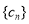 是“和等比数列”,则
是“和等比数列”,则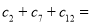 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com