
求证: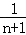 +
+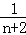 +…+
+…+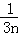 >
>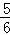 (n≥2,n∈N*).
(n≥2,n∈N*).
科目:高中数学 来源:[同步]2015年北师大版必修二 2.3空间直角坐标系练习卷(解析版) 题型:解答题
在空间直角坐标系中,解答下列各题:
(1)在x轴上求一点P,使它与点P0(4,1,2)的距离为 ;
;
(2)在xOy平面内的直线x+y=1上确定一点M,使它到点N(6,5,1)的距离最小.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年北师大版必修一 3.1 正整数指数函数练习卷(解析版) 题型:填空题
当x∈N+时,用“>”“<”或“=”填空:
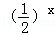 1,2x 1,
1,2x 1,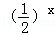 2x,
2x,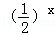
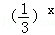 ,2x 3x.
,2x 3x.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年北师大版必修一 2.1 生活中的变量关系练习卷(解析版) 题型:选择题
某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在如图中纵轴表示离学校的距离,横轴表示出发后的时间,则如图中的四个图形中较符合该学生走法的是( )
A.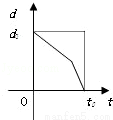 B.
B.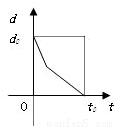 C.
C. D.
D.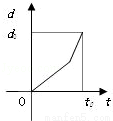
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版选修4-5 3.1 数学归纳法原理练习卷(解析版) 题型:解答题
已知函数f(x)=x3﹣x2+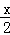 +
+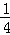 ,且存在x0∈(0,
,且存在x0∈(0,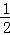 ),使f(x0)=x0.
),使f(x0)=x0.
(1)证明:f(x)是R上的单调增函数;
(2)设x1=0,xn+1=f(xn);y1=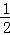 ,yn+1=f(yn),其中n=1,2,…,证明:xn<xn+1<x0<yn+1<yn;
,yn+1=f(yn),其中n=1,2,…,证明:xn<xn+1<x0<yn+1<yn;
(3)证明: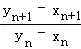 <
<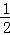 .
.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版选修4-5 3.1 数学归纳法原理练习卷(解析版) 题型:填空题
用数学归纳法证明:“1×4+2×7+3×10+…+n(3n+1)=n(n+1)2,n∈N+”,当n=1时,左端为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版选修4-5 3.1 数学归纳法原理练习卷(解析版) 题型:选择题
某个命题与自然数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立.现已知当n=5时,该命题不成立,那么可推得( )
A.当n=6时,该命题不成立 B.当n=6时,该命题成立
C.当n=4时,该命题不成立 D.当n=4时,该命题成立
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版必修二2.4 空间直角坐标系练习卷(解析版) 题型:解答题
已知A(1,﹣2,11),B(4,2,3),C(6,﹣1,4),求证其为直角三角形.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教A版选修1-1 3.4生活中的优化问题举例练习卷(解析版) 题型:填空题
如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是 .
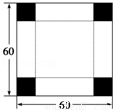
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com