6
分析:有点M的坐标可知点M在以(2,0)为圆心,半径为5的大圆上,给出的圆C和点M的轨迹是同心圆,由
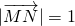
可知N的轨迹是圆心在M的轨迹上,半径为1的圆,画出图形后,利用对称性取N的轨迹与x轴的左交点,分析得到N取该点时能使
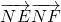
的值最小.
解答:
解:设M(x,y),由M(2+5cosθ,5sinθ),所以
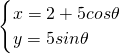
,
整理得:(x-2)
2+y
2=25.故点M在一个圆心为(2,0),半径为5的大圆上,这个大圆与圆C:(x-2)
2+y
2=4是同心圆.
又点N满足
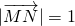
,所以点N的轨迹为(x-2-5cosθ)
2+(y-5sinθ)
2=1.
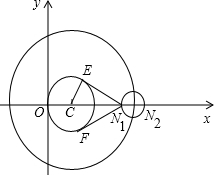
基于对称性,我们取一个较为方便的位置进行研究.如图,
取θ=0,此时圆N的圆心为(7,0),于是N点在(x-7)
2+y
2=1的小圆上,这个小圆与x轴有两个交点,左边的交点N
1(6,0);右边的交点N
2(8,0).因为N
1离圆C最近,因此切线最短,两条切线的夹角α最大,且α是锐角,cosα是减函数,因此由N
1作出的两条切线向量的模最小,cosα的值最小,故数量积
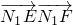
必是最小.
在RT△CEN
1中,CN
1=4,CE=2,故
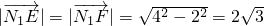
,cos

=

,
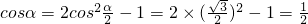
.
∴
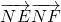
的最小值为
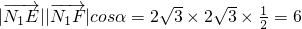
.
故答案为6.
点评:本题考查了平面向量数量积的运算,考查了圆的参数方程,体现了数形结合的解题思想,解答此题的关键是读懂题目意思,属中档题.

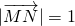 ,过N作圆C:(x-2)2+y2=4的两条切线NE,NF,切点分别为E,F,则
,过N作圆C:(x-2)2+y2=4的两条切线NE,NF,切点分别为E,F,则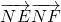 的最小值为________.
的最小值为________.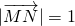 可知N的轨迹是圆心在M的轨迹上,半径为1的圆,画出图形后,利用对称性取N的轨迹与x轴的左交点,分析得到N取该点时能使
可知N的轨迹是圆心在M的轨迹上,半径为1的圆,画出图形后,利用对称性取N的轨迹与x轴的左交点,分析得到N取该点时能使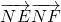 的值最小.
的值最小. 解:设M(x,y),由M(2+5cosθ,5sinθ),所以
解:设M(x,y),由M(2+5cosθ,5sinθ),所以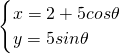 ,
,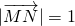 ,所以点N的轨迹为(x-2-5cosθ)2+(y-5sinθ)2=1.
,所以点N的轨迹为(x-2-5cosθ)2+(y-5sinθ)2=1.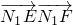 必是最小.
必是最小.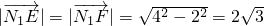 ,cos
,cos =
= ,
,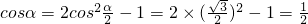 .
.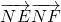 的最小值为
的最小值为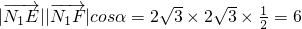 .
.

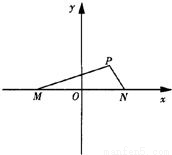
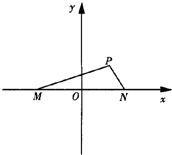 如图,已知在坐标平面内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为
如图,已知在坐标平面内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为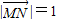 ,过N作圆C:(x-2)2+y2=4的两条切线NE,NF,切点分别为E,F,则
,过N作圆C:(x-2)2+y2=4的两条切线NE,NF,切点分别为E,F,则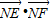 的最小值为 .
的最小值为 .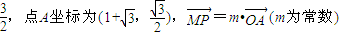 ,
,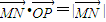 .
.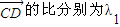 、λ2,求证:λ1+λ2=0.
、λ2,求证:λ1+λ2=0.