解:
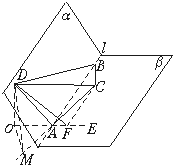
(1)过D向平面β作垂线,垂足为O,连接OA并延长至E,
∵AB⊥AD,OA为DA在平面β内的射影,
∴AB⊥OA,∴∠DAE为二面角α-l-β的平面角 (2分)
∴∠DAE=120°,∠DAO=60°,
∵AD=AB=2,∴Rt△ADO中,DO=ADsin60°=

,
∵△ABC是等腰直角三角形,斜边AB=2.
∴S
△ABC=

×2×1=1,
又∵D到平面β的距离DO=

,
∴V
D-
ABC=

×S
△ABC×DO=

.(4分)
(2)过O在β内作OM⊥AC于M,连接DM,则AC⊥DM,
∴∠DMO为二面角D-AC-B的平面角,(6分)
在△DOA中,OA=2cos60°=1,且∠OAM=∠CAE=45°,
∴Rt△OAM中,OM=OAsin45°=

,
∴Rt△ODM中,tan∠DMO=
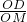
=

,
因此,∠DMO=arctan

,即二面角D-AC-B的大小为arctan

.(8分)
(3)在β内过C作AB的平行线交AE于F,
∴∠DCF(或其补角)为异面直线AB、CD所成的角 (10分)
∵AB⊥AF,AB⊥AD,CF∥AB,
∴CF⊥DF,结合∠CAE=45°,得△ACF为等腰直角三角形,
又∵AF等于C到AB的距离,即为△ABC斜边上的高,
∴AF=CF=

AB=1,
∴DF
2=AD
2+AF
2-2AD•AF•cos120°=7,得DF=

在Rt△DCF中,tan∠DCF=
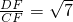
,得∠DCF=arctan

,
即异面直线AB、CD所成的角为arctan

.(12分)
分析:(1)过D作DO⊥β于点O,连接OA并延长至E,可证出∠DAE为二面角α-l-β的平面角,得∠DAO=180°-120°=60°.Rt△ADO中,算出DO=

,即为三棱锥D-ABC的高,最后算出△ABC的面积,再利用锥体体积公式即得三棱锥D-ABC体积;
(2)过O在β内作OM⊥AC于M,连接DM,则AC⊥DM,得∠DMO为二面角D-AC-B的平面角.然后在Rt△ODM中,算出OM的长.Rt△ODM中利用直角三角形中正切的定义,得tan∠DMO=

,即得二面角D-AC-B的大小为arctan

;
(3)在β内过C作CE∥AB交AE于F,可得∠DCF(或其补角)为异面直线AB、CD所成的角.Rt△DCF中,算出CF、DF的长,从而得到tan∠DCF=
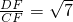
,即得异面直线AB、CD所成的角为arctan

.
点评:本题给出120度的二面角和分别在两个半平面的等腰直角三角形,求三棱锥的体积和异面直线所成角的大小,着重考查了二面角平面角的作法和异面直线所成角的求法等知识,考查了解三角形的知识,属于中档题.

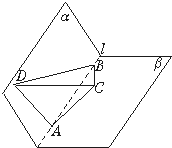 如图α-l-β是120°的二面角,A、B两点在棱l上,AB=2,D在α内,三角形ABD是等腰直角三角形,∠DAB=90°,C在β内,三角形ABC是等腰直角三角形,∠ACB=90°.
如图α-l-β是120°的二面角,A、B两点在棱l上,AB=2,D在α内,三角形ABD是等腰直角三角形,∠DAB=90°,C在β内,三角形ABC是等腰直角三角形,∠ACB=90°. (1)过D向平面β作垂线,垂足为O,连接OA并延长至E,
(1)过D向平面β作垂线,垂足为O,连接OA并延长至E, ,
, ×2×1=1,
×2×1=1, ,
, ×S△ABC×DO=
×S△ABC×DO= .(4分)
.(4分) ,
,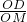 =
= ,
, ,即二面角D-AC-B的大小为arctan
,即二面角D-AC-B的大小为arctan .(8分)
.(8分) AB=1,
AB=1,
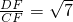 ,得∠DCF=arctan
,得∠DCF=arctan ,
, .(12分)
.(12分) ,即为三棱锥D-ABC的高,最后算出△ABC的面积,再利用锥体体积公式即得三棱锥D-ABC体积;
,即为三棱锥D-ABC的高,最后算出△ABC的面积,再利用锥体体积公式即得三棱锥D-ABC体积; ,即得二面角D-AC-B的大小为arctan
,即得二面角D-AC-B的大小为arctan ;
;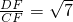 ,即得异面直线AB、CD所成的角为arctan
,即得异面直线AB、CD所成的角为arctan .
.

 名校课堂系列答案
名校课堂系列答案 如图,F是椭圆
如图,F是椭圆 如图,F是椭圆
如图,F是椭圆 (2013•惠州模拟)如图,A,B是椭圆
(2013•惠州模拟)如图,A,B是椭圆 如图,点F是椭圆W:
如图,点F是椭圆W: