
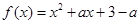 ,其中
,其中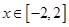 。
。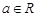 时,讨论它的单调性;
时,讨论它的单调性;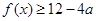 恒成立,求
恒成立,求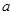 的取值范围.
的取值范围.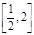 (2)当
(2)当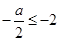 得
得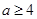 ,
,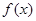 单调增区间为
单调增区间为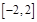 ;当
;当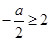 得
得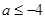 ,
,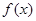 单调减区间为
单调减区间为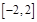 ;当
;当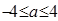 时,
时,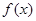 单调增区间为
单调增区间为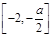 ,单调减区间为
,单调减区间为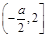 . (3)
. (3)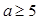
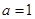 时,
时,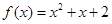 ,对称轴方程为
,对称轴方程为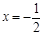 ,
,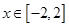 在对称轴方程
在对称轴方程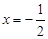 内,则
内,则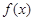 的单调减区间为
的单调减区间为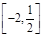 ;
;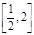 5分
5分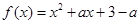 ,对称轴方程为
,对称轴方程为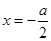 ,
,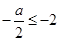 得
得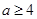 ,
,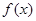 单调增区间为
单调增区间为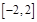 ;
;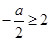 得
得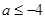 ,
,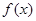 单调减区间为
单调减区间为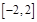 ;
;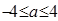 时,
时,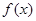 单调增区间为
单调增区间为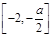 ,单调减区间为
,单调减区间为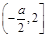 . 10分
. 10分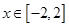 时,有
时,有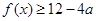 恒成立,
恒成立,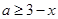 ,只要
,只要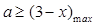 ,
,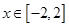 ,
,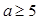 15分
15分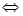

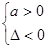 ;f(x)<0恒成立
;f(x)<0恒成立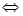

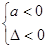 .若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.
.若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:不详 题型:解答题
 小时的收费为
小时的收费为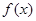 元
元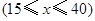 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动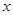 小时的收费为
小时的收费为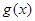 元
元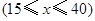 .试求
.试求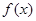 和
和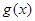 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
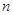 个月的维修费为
个月的维修费为 元,买这种冰激凌机花费
元,买这种冰激凌机花费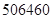 元,使用
元,使用 年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( )
年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( ) 机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;
机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;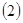 一年按
一年按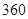 天计算.)
天计算.)A.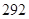 元 元 | B.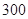 元 元 | C.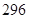 元 元 | D.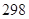 元 元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
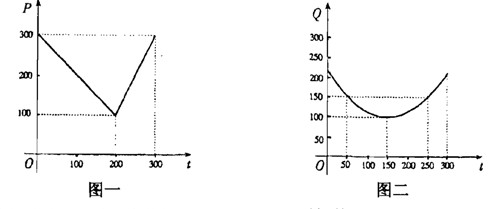
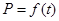 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式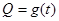 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com