
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图),![]() 为
为![]() 中点.
中点.
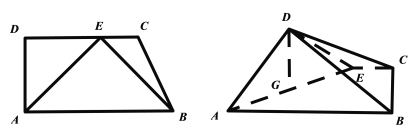
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)详见解析;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)根据面面垂直的性质定理,证得![]() 平面
平面![]() .
.
(2)作出直线![]() 与平面
与平面![]() 所成的角,解三角形求得线面角的正弦值.
所成的角,解三角形求得线面角的正弦值.
(3)设![]() 是
是![]() 靠近
靠近![]() 的四等分点,
的四等分点,![]() 是
是![]() 靠近
靠近![]() 的四等分点,通过证明平面
的四等分点,通过证明平面![]() 平面
平面![]() ,证得
,证得![]() 平面
平面![]() ,并由此求得
,并由此求得![]() 的值.
的值.
(1)由于![]() ,
,![]() 是
是![]() 的中点,所以
的中点,所以![]() ,由于平面
,由于平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)连接![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,所以
,所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角.
所成的角.![]() .在三角形
.在三角形![]() 中,
中,![]() ,由余弦定理得
,由余弦定理得![]()
![]() .在
.在![]() 中,
中,![]() ,所以
,所以![]() .所以
.所以![]() .
.
(3)存在,且![]() 是
是![]() 靠近
靠近![]() 的四等分点.
的四等分点.
设![]() 是
是![]() 靠近
靠近![]() 的四等分点,
的四等分点,![]() 是
是![]() 靠近
靠近![]() 的四等分点,连接
的四等分点,连接![]() .
.
由于![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
由于![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
由于![]() ,所以
,所以![]() ,由于
,由于![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
由于![]() ,根据面面平行的判定定理可知,平面
,根据面面平行的判定定理可知,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故存在![]() 是
是![]() 靠近
靠近![]() 的四等分点,使
的四等分点,使![]() 平面
平面![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB=4,E为BC的中点,现将△BAE与△DCE折起,使得平面BAE及平面DEC都与平面ADE垂直.

(1)求证:BC∥平面ADE;
(2)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在打击拐卖儿童犯罪的活动中,警方救获一名男孩,为了确定他的家乡,警方进行了调查:
知情人士A说,他可能是四川人,也可能是贵州人;
知情人士B说,他不可能是四川人;
知情人士C说,他肯定是四川人;
知情人士D说,他不是贵州人.
警方确定,只有一个人的话不可信.根据以上信息,警方可以确定这名男孩的家乡是( )
A.四川B.贵州
C.可能是四川,也可能是贵州D.无法判断
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷是19世纪德国著名的数学家,他定义了一个“奇怪的函数” ,下列关于狄利克雷函数的叙述正确的有:______.
,下列关于狄利克雷函数的叙述正确的有:______.
①![]() 的定义域为
的定义域为![]() ,值域是
,值域是![]() ②
②![]() 具有奇偶性,且是偶函数
具有奇偶性,且是偶函数
③![]() 是周期函数,但它没有最小正周期 ④对任意的
是周期函数,但它没有最小正周期 ④对任意的![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,满足:
中,满足:![]() ,M是
,M是![]() 的中点.
的中点.
(1)若![]() ,求向量
,求向量![]() 与向量
与向量![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若O是线段![]() 上任意一点,且
上任意一点,且![]() ,求
,求![]() 的最小值:
的最小值:
(3)若点P是![]() 内一点,且
内一点,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com