
(本小题满分12分)
图4是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图
(Ⅰ)求直方图中x的值
(II)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用水量在3至4吨的居民数X的分布列和数学期望。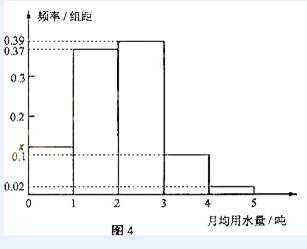
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):
| | 物理成绩好 | 物理成绩不好 | 合计 |
| 数学成绩好 | 20 | 30 | 50 |
| 数学成绩不好 | 40 | a | 60 |
| 合计 | 60 | 50 | 110 |
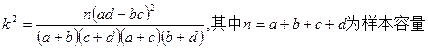
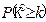 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(10分)假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
| x | 2 | 3 | 4 | 5 | 6 |
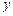 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.
(Ⅰ)求该班学生参加活动的人均次数 ;
;
(Ⅱ)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅲ)从该班中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望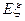 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
(1) 试分别估计两个分厂生产的零件的优质品率;
(2) 由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| | 甲 厂 | 乙 厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合计 | | | |



查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)某种产品的广告费用支出X与销售额y(百万元)之间有如下对应数据:
| X | 2 | 4 | 5 | 6 | 8 |
| Y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表。
| 序号(i) | 分组(睡眠时间) | 频数(人数) | 频率 |
| 1 | [4,5) | 6 | 0.12 |
| 2 | [5,6) | | 0.20 |
| 3 | [6,7) | a | |
| 4 | [7,8) | b | |
| 5 | [8,9) | | 0.08 |
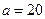 ,将表中数据补全,并画出频率分布直方图.
,将表中数据补全,并画出频率分布直方图.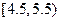 的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求
的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求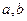 的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.
的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(Ⅰ) 完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com