某市2010年4月1日—4月30日对空气污染指数的监测数据如下（主要污染物为可吸入颗粒物）:
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(Ⅰ) 完成频率分布表；
（Ⅱ）作出频率分布直方图；
（Ⅲ）根据国家标准，污染指数在0~50之间时，空气质量为优：在51~100之间时，为良；在101~150之间时，为轻微污染；在151~200之间时，为轻度污染。
请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价.
科目：高中数学 来源： 题型：解答题
某教师出了一份共3道题的测试卷，每道题1分。全班的3分、2分、1分和0分的学生所占的比例分别为30%，50%，10%和10%。
（1）若全班共10人，则平均分是多少？
（2）若全班共20人，则平均分是多少？
（3）若该班人数未知，能求出该班的平均分吗？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段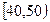
，
…
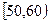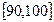后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（1）求第四小组的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；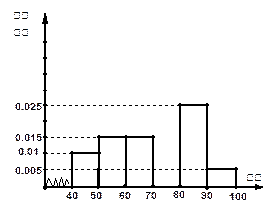
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某次运动会甲、乙两名射击运动员成绩如下：
甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；
乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；
（1）用茎叶图表示甲，乙两个成绩；
（2）根据茎叶图分析甲、乙两人成绩；
（3）分别计算两个样本的平均数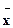
和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料：
| 日 期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差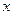 （°C） | 10 | 11 | 13 | 12 | 8 |
发芽数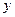 （颗） | 23 | 25 | 30 | 26 | 16 |
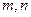，求事件“m ，n均不小于25”的概率.
；
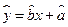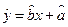，其中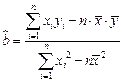
，
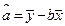，）查看答案和解析>>
科目：高中数学 来源： 题型：解答题
对400个某种型号的电子元件进行寿命追踪调查，其频率分布表如下表：
| 寿命（h） | 频率 |
| 500600 | 0.10 |
| 600700 | 0.15 |
| 700800 | 0.40 |
| 800900 | 0.20 |
| 9001000 | 0.15 |
| 合计 | 1 |
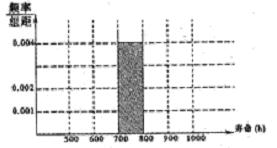
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
一个乒乓球队里有男队员5人，女队员4人，从中选出男、女队员各一名组成混合双打，不同的选法共有（ ）
| A．9种 | B．10种 | C．15种 | D．20种 |
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
图4是某城市通过抽样得到的居民某年的月均用水量（单位：吨）的频率分布直方图
（Ⅰ）求直方图中x的值
（II）若将频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用水量在3至4吨的居民数X的分布列和数学期望。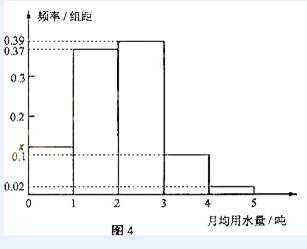
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
展开式中含的有理项共有（ ）