练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量a＝(1，k)，b＝(2,2)，且a＋b与a共线，那么a·b的值为(　　)

    A．1 B．2 C．3 D．4

     

    D

    【解析】a＋b＝(3，k＋2)，由共线知3k－(k＋2)＝0，k＝1，

    ∴a·b＝4，选D项．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-2等差数列及其前n项和（解析版） 题型：填空题

    已知数列{an}为等差数列，若<－1，且它们的前n项和Sn有最大值，则使Sn>0的n的最大值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-3平面向量的数量积及应用（解析版） 题型：选择题

    已知向量a，b的模都是2，其夹角为60°，又知＝3a＋2b，＝a＋3b，则P，Q两点间的距离为(　　)

    A．2 B． C．2 D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-2平面向量的基本定理及坐标表示（解析版） 题型：选择题

    如图，＝(6,1)，＝(x，y)，＝(－2，－3)，若∥且⊥，则四边形ABCD的面积S为(　　)

    A．16 B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-2平面向量的基本定理及坐标表示（解析版） 题型：选择题

    已知向量a＝(2,1)，b＝(1，k)，且a与b的夹角为锐角，则实数k的取值范围是(　　)

    A．(－2，＋∞) B．(－2，)∪(，＋∞)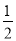

    C．(－∞，－2) D．(－2,2)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-1向量的概念及运算（解析版） 题型：解答题

    设a、b是不共线的两个非零向量，

    (1)若＝2a－b，＝3a＋b，＝a－3b，求证：A、B、C三点共线；

    (2)若8a＋kb与ka＋2b共线，求实数k的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-1向量的概念及运算（解析版） 题型：选择题

    设a、b都是非零向量，下列四个条件中，使＝成立的充分条件是(　　)

    A．|a|＝|b|且a∥b B．a＝－b

    C．a∥b D．a＝2b

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-8解三角形应用举例（解析版） 题型：选择题

    某人先向正东方向走了x km，然后他向右转150°，向新的方向走了3 km，结果他离出发点恰好为km，那么x的值为(　　)

    A． B．2 C．2或 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-5两角和与差的正弦、余弦和正切（解析版） 题型：填空题

    已知α为锐角，且cos(α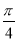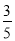＋)＝，则sinα＝________．

     

    查看答案和解析>>

    同步练习册答案