解:∵不等式|x-
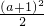
|≤
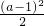
,∴-
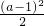
≤
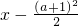
≤
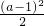
,
即 2a≤x≤a
2+1,∴A=[2a,a
2+1]. (5分)
由 x
2-3(a+1)x+2(3a+1)≤0 得 (x-2)[x-(3a+1)]≤0.
令(x-2)[x-(3a+1)]=0 得 x
1=2,x
2=3a+1.
当2<3a+1,即a>

时,B={x|2≤x≤3a+1},
当2>3a+1,即x<

时,B={x|3a+1≤x≤2},
当2=3a+1,即a=

时,B={2}.(10分)
要使A⊆B,当A=∅时,a
2+1<2a,此时 (a-1)
2<0,不可能出现此种情况.所以A≠∅,
当a>

时,2a≥2且a
2+1≤3a+1,所以1≤a≤3.
当 a<

时,2a≥3a+1且a
2+1≤2,所以a=-1.
当 a=

时,2a=2且a
2+1=2,所以a∈∅.
综上所述:a的取值范围是{a|1≤a≤3或a=-1}.(20分)
分析:解一元二次不等式求出集合A,解一元二次不等式,分2<3a+1、2>3a+1、2=3a+1三种情况分别求出集合B,由A⊆B,考查两个区间的端点间的大小关系,求出a的取值范围.
点评:本题主要考查集合关系中参数的取值范围问题,体现了分类讨论的数学思想,绝对值不等式、一元二次不等式的解法,属于中档题.

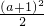 |≤
|≤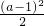 与x2-3(a+1)x+2(3a+1)≤0的解集分别为A,B,其中a∈R.,求使A⊆(A∩B)的a 的取值范围.
与x2-3(a+1)x+2(3a+1)≤0的解集分别为A,B,其中a∈R.,求使A⊆(A∩B)的a 的取值范围.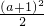 |≤
|≤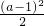 ,∴-
,∴-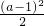 ≤
≤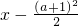 ≤
≤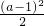 ,
, 时,B={x|2≤x≤3a+1},
时,B={x|2≤x≤3a+1}, 时,B={x|3a+1≤x≤2},
时,B={x|3a+1≤x≤2}, 时,B={2}.(10分)
时,B={2}.(10分) 时,2a≥2且a2+1≤3a+1,所以1≤a≤3.
时,2a≥2且a2+1≤3a+1,所以1≤a≤3. 时,2a≥3a+1且a2+1≤2,所以a=-1.
时,2a≥3a+1且a2+1≤2,所以a=-1. 时,2a=2且a2+1=2,所以a∈∅.
时,2a=2且a2+1=2,所以a∈∅.
