练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

        如图，M—l—N是120°的二面角，A、B两点在棱上，AB=2，D在平面M内，三角形ABD是等腰直角三角形，∠DAB=90°,C在N内,三角形ABC是直角三角形，∠ACB=90°，∠ABC=60°.

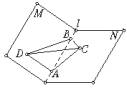
        （1）求三棱锥D—ABC的体积；

        （2）求直线BD与平面N所成的角的正弦值；

        （3）求二面角D—AC—B的平面角的正切值.

     

    答案：
    解析：

    答案：解：（1）过D向平面N作垂线，垂足为O，连接OA并延长至E.

        ∵AB⊥AD，OA为DA在平面N内的射影，

        ∴AB⊥OA.∴∠DAE为二面角M—l—N的平面角.

        ∴∠DAE=120°.∴∠DAO=60°.

        ∵AD=AB=2，∴.

        ∵△ABC是有一个锐角为30°的直角三角形，斜边AB=2，

        ∴，又D到平面N的距离.

        ∴.

        （2）由（1）可知，∠DBO为直线BD与平面N所成的角，

        ∴.

        （3）过O在N内作OF⊥AC，交AC的反向延长线于F，连接DF，则AC⊥DF，

        ∴∠DFO为二面角D—AC—B的平面角.又在△DOA中，OA=2cos60°=1，即∠OAF=

        ∠EOC=60°，∴OF=1·sin60°=.

        ∴.

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

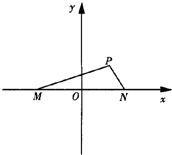    精英家教网如图，已知在坐标平面内，M、N是x轴上关于原点O对称的两点，P是上半平面内一点，△PMN的面积为
    3
    2
    ，点A坐标为(1+
    		3
    ，
    		3
    2
    )，
    MP
    =m•
    OA
    (m为常数)    ，
    MN
    •
    OP
    =|
    MN
    |    ．
    （Ⅰ）求以M、N为焦点且过点P的椭圆方程；
    （Ⅱ）过点B（-1，0）的直线l交椭圆于C、D两点，交直线x=-4于点E，点B、E分
    CD
    的比分别为λ1    、λ2，求证：λ1+λ2=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的中心在坐标原点，焦点在x轴上，左、右焦点分别为F1，F2，且|F1F2|=2，点P（1，
    32
    ）在椭圆C上．
    （I）求椭圆C的方程；
    （II）如图，动直线l：y=kx+m与椭圆C有且仅有一个公共点，点M，N是直线l上的两点，且F1M⊥l，F2M⊥l，求四边形F1MNF2面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图：过抛物线y2=4x上的点A（1，2）作切线l交x轴与直线x=-4分别于D，B．动点P是抛物线y2=4x上的一点，点E在线段AP上，满足
    AE
    EP
    =λ1    ；点F在线段BP上，满足
    BF
    FP
    =λ2    ，3λ1+2λ2=15且在△ABP中，线段PD与EF交于点Q．
    （1）求点Q的轨迹方程；
    （2）若M，N是直线x=-3 上的两点，且⊙O1：（x+2）2+y2=1是△QMN的内切圆，试求△QMN面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

        如图，M—l—N是120°的二面角，A、B两点在棱上，AB=2，D在平面M内，三角形ABD是等腰直角三角形，∠DAB=90°,C在N内,三角形ABC是直角三角形，∠ACB=90°，∠ABC=60°.

        （1）求三棱锥D—ABC的体积；

        （2）求直线BD与平面N所成的角的正弦值；

        （3）求二面角D—AC—B的平面角的正切值.

     

    查看答案和解析>>

    同步练习册答案