练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线y=2x是△ABC中∠BCA的平分线所在的直线,若A、B两点的坐标分别为A(-4,2)、B(3,1),求点C的坐标.

    思路解析：可以考虑AC到平分线的角与平分线到BC的角相等；也可以利用AC、BC关于平分线对称来解决.

    解法一:AB所在直线方程为=,即x+7y-10=0.设∠BCA的平分线与直线AB交于点D(x,y),解方程组得D点坐标(,).设C(x0,2x0),由CD为∠BCA的平分线得||=||.

    即=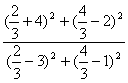.整理得3x02-8x0+4=0.

    解之,得x0=(舍去)或x0=2.∴C点坐标为(2,4).

    解法二:设C点坐标为(x0,2x0),则kAC=,kBC=.由题意得=,即=.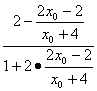

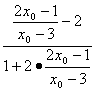    整理,得2x0-2=x0.∴x0=2.∴点C坐标为(2,4).

    解法三:由题意知,点A关于直线y=2x的对称点A′在BC所在直线上,设A′点坐标为(x1,y1),则它满足=-,即x1=-2y1.                                                 ①

    =2·,即2x1-y1-10=0.                               ②

    解①②两式组成的方程组,得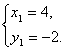

    ∴BC所在直线方程为=,即3x+y-10=0.

    解方程组,得.∴所求C点坐标为(2,4).


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    直线y=2x+m和圆x2+y2=1交于点A、B，以x轴的正方向为始边，OA为终边（O是坐标原点）的角为α，OB为终边的角为β，若|AB|=
    		3
    ，那么sin（α-β）的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出以下几个命题：
    ①由曲线y=x2与直线y=2x围成的封闭区域的面积为
    4
    3
    ；
    ②已知点A是定圆C上的一个定点，线段AB为圆的动弦，若
    OP
    =
    1
    2
    (
    OA
    +
    OB
    )    ，O为坐标原点，则动点P的轨迹为圆；
    ③把5本不同的书分给4个人，每人至少1本，则不同的分法种数为A54•A41=480种；
    ④若直线l∥平面α，直线l⊥直线m，直线l?平面β，则β⊥α．
    其中，正确的命题有
     
    ．（将所有正确命题的序号都填在横线上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线y2=4x与直线y=2x+b相交于A，B两点，|AB|=3
    		5
    ．
    （1）求b的值；
    （2）设P 是x轴上的一点，当△PAB的面积为39时，求点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C的圆心在直线y=2x上，且与直线l：x+y+1=0相切于点P（-1，0）．
    （Ⅰ）求圆C的方程；
    （Ⅱ）若A（1，0），点B是圆C上的动点，求线段AB中点M的轨迹方程，并说明表示什么曲线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线Y=2X+b与曲线XY=2相交于A，B两点，若|AB|=5，则实数b的值是（　　）

    查看答案和解析>>

    同步练习册答案