Question

如图所示，自点A(-3，3)发出的光线l射到x轴上，被x轴反射，其反射光线所在直线与圆x²+y²-4x-4y+7=0相切，求光线l所在直线的方程.

Answer 1

思路解析：根据入射角等于反射角可以求出反射光线的斜率;也可以考虑利用对称来求解.

解法一：由已知，圆的标准方程为(x-2)²+(y-2)²＝1.

设光线l所在直线的方程为y-3=k(x+3).

由题意知k≠0，于是l的反射点的坐标是B(-，0).

 因为光线入射角等于反射角，所以反射光线l′所在直线的方程是 y=-k［x+］.整理，得kx+y+3k+3＝0.

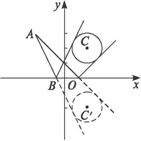
这条直线与已知圆相切，如图所示，因而圆心到它的距离等于半径1.

即=1,12k²+25k+12=0.

解得k=-，或k=-.

故所求直线方程为y-3＝-(x+3)，或y-3＝-(x+3)，

即3x+4y-3＝0，或4x+3y+3＝0.

本题也可先求圆C关于x轴的对称圆方程，再利用对称圆的圆心C′到入射光线所在直线的距离等于圆C的半径求斜率k，得所求直线方程，如图，从而有以下另一解法.

解法二：∵圆C：(x-2)²+(y-2)²＝1，

∴圆C关于x轴的对称圆C′为(x-2)²+(y+2)²=1.

令l：y-3＝k(x+3)，则kx-y+3+3k=0，

∴1=.

∴k=-，或k=-.

∴l：3x+4y-3＝0，或4x+3y+3=0.

解法三:设A关于x轴的对称点为A′，则A′(-3，-3).

A′点在反射光线l′上.

设反射光线的斜率为k，则其方程为

y+3＝k(x+3)，即kx-y+3k-3=0.

由直线与圆相切，∴=1.

解得k＝，或k=，

∴l′：4x-3y+3＝0或3x-4y-3=0.

令y=0,得x＝或x＝，即l′与x轴交点为(，0)或(，0)，由两点式可得 l的方程为3x+4y-3=0或4x+3y+3=0.

深化升华

    光线反射问题，常常考虑对称；而圆的切线问题则常用几何法，即考虑圆心到直线的距离和半径的大小关系.