
 圆
圆 与
与 轴正半轴的交点为
轴正半轴的交点为 ,与曲线
,与曲线 的交点为
的交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 .
. 表示
表示 和
和
 满足
满足
 的值,使得数列
的值,使得数列 成等比数列;
成等比数列; 与
与 的大小.
的大小.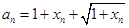 ,
,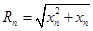 ;(2)当
;(2)当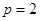 时,数列
时,数列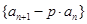 成公比为4的等比数列;当
成公比为4的等比数列;当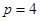 时,数列
时,数列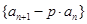 成公比为2的等比数列.
成公比为2的等比数列.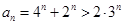 .
. 和圆中,联立得到
和圆中,联立得到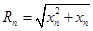 ,由于直线MN过M、A点,从而得到直线MN的方程,N点也在MN上,代入MN方程中,经整理得到
,由于直线MN过M、A点,从而得到直线MN的方程,N点也在MN上,代入MN方程中,经整理得到 的表达式;第二问,(ⅰ)利用等比数列的定义知
的表达式;第二问,(ⅰ)利用等比数列的定义知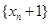 为等比数列,利用等比数列的通项公式,经过化简得
为等比数列,利用等比数列的通项公式,经过化简得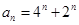 ,利用
,利用 的通项公式和
的通项公式和 为等比数列列出2个关系式,利用2个式子是q倍的关系,解出p和q的值;(ⅱ)利用
为等比数列列出2个关系式,利用2个式子是q倍的关系,解出p和q的值;(ⅱ)利用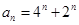 可以猜想
可以猜想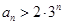 ,即需要证
,即需要证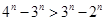 ,构造函数
,构造函数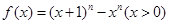 ,利用导数判断函数
,利用导数判断函数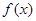 的单调性,从而确定
的单调性,从而确定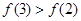 ,即
,即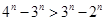 ,所以
,所以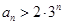 .
. 与圆
与圆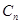 交于点
交于点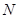 ,则
,则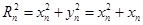 ,即
,即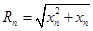 .由题可知,点
.由题可知,点 的坐标为
的坐标为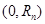 ,从而直线
,从而直线 的方程为
的方程为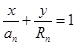 ,由点
,由点 在直线
在直线 上得
上得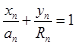 ,将
,将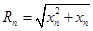 ,
,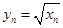 代入,
代入, 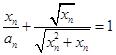 ,
, 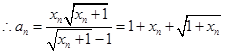 即
即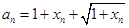 4分
4分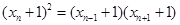 知,
知,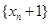 为等比数列,由
为等比数列,由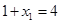 ,
,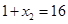 知,公比为4,故
知,公比为4,故 ,所以
,所以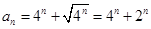 5分
5分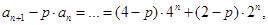
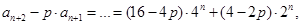

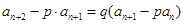 得
得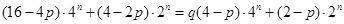
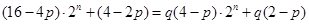
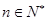 成立,得
成立,得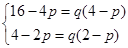 解得
解得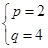 或
或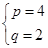 8分
8分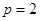 时,数列
时,数列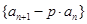 成公比为4的等比数列;
成公比为4的等比数列;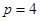 时,数列
时,数列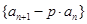 成公比为2的等比数列. 9分
成公比为2的等比数列. 9分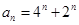 ,当
,当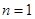 时,
时,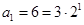 ;当
;当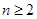 时,
时,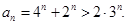 事实上,令
事实上,令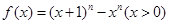 ,则
,则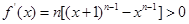 故
故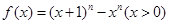 是增函数,所以
是增函数,所以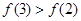 ,即
,即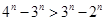
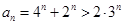 . 14分
. 14分

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:不详 题型:单选题
| A.(0,1] | B.[1,+∞) |
| C.(-∞,-1]∪(0,1] | D.[-1,0)∪(0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com