
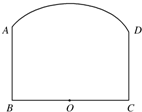
 如图,钢板材料ABCD的上沿为圆弧AD,其所在圆的圆心为BC的中点O,AB、CD都垂直于BC,且AB=CD=a,BC=b,现如何用这块钢板材料截一块矩形板(其中两个顶点在
如图,钢板材料ABCD的上沿为圆弧AD,其所在圆的圆心为BC的中点O,AB、CD都垂直于BC,且AB=CD=a,BC=b,现如何用这块钢板材料截一块矩形板(其中两个顶点在 | AD |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
a2+
|
| a |
| R |
| b |
| 2R |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| a |
| R |
| b |
| 2R |
| π |
| 4 |
| 1 |
| 4 |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
 (2012•江苏一模)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
(2012•江苏一模)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)查看答案和解析>>
科目:高中数学 来源: 题型:
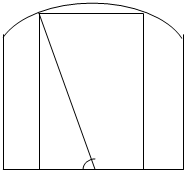 如图,钢板材料ABCD,上沿为圆弧AD,其所在圆的圆心为BC中点O,AB、CD都垂直于BC,且AB=CD=
如图,钢板材料ABCD,上沿为圆弧AD,其所在圆的圆心为BC中点O,AB、CD都垂直于BC,且AB=CD=| 3 |
查看答案和解析>>
科目:高中数学 来源:《3.2 简单的三角恒等变换》2013年同步练习2(解析版) 题型:解答题
 上,另两个顶点在BC上),使矩形的面积最大?请你设计截取方案,并说明理由.
上,另两个顶点在BC上),使矩形的面积最大?请你设计截取方案,并说明理由.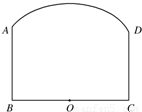
查看答案和解析>>
科目:高中数学 来源:2007-2008学年浙江省宁波市高一(上)期末数学试卷(解析版) 题型:解答题
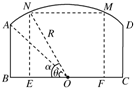
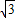 米,BC=2米,现要用这块钢板材料截成一块矩形板EFGH(其中G,H在AD上,E,F在BC上),设∠BOH=θ.
米,BC=2米,现要用这块钢板材料截成一块矩形板EFGH(其中G,H在AD上,E,F在BC上),设∠BOH=θ.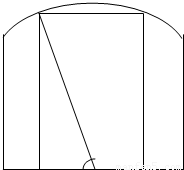
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com