
【题目】已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>﹣2f(x),若g(x)=x2f(x),则不等式g(x)<g(1﹣x)的解集是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(﹣∞,0)∪(0, ![]() )
)
D.(0, ![]() )
)
【答案】C
【解析】解:∵f(x)是定义域为{x|x≠0}的偶函数,
∴f(﹣x)=f(x).
对任意正实数x满足xf′(x)>﹣2f(x),
∴xf′(x)+2f(x)>0,
∵g(x)=x2f(x),
∴g′(x)=2xf(x)+x2f′(x)>0.
∴函数g(x)在(0,+∞)上单调递增,
∴g(x)在(﹣∞,0)递减;
由不等式g(x)<g(1﹣x),
∴ 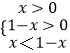 或
或 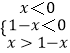 ,
,
解得:0<x< ![]() ,或x<0
,或x<0
∴不等式g(x)<g(1﹣x)的解集为:{x|0<x< ![]() 或x<0}.
或x<0}.
故选:C.
【考点精析】利用导数的几何意义和利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图像与
的图像与![]() 轴的交点为
轴的交点为![]() ,在
,在![]() 轴右侧的第一个最高点和第一个与
轴右侧的第一个最高点和第一个与![]() 轴交点分别为
轴交点分别为![]()
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 图像上所有点的横坐标变为原来的
图像上所有点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图像沿
倍(纵坐标不变),再将所得图像沿![]() 轴正方向平移
轴正方向平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像,求
的图像,求![]() 的解析式;
的解析式;
(3)在(2)的条件下求函数![]() 在
在![]() 上的值域。
上的值域。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com