
| 6-h |
| 2π |
| 1 |
| 8π |
| 6-h |
| 2π |
| 1 |
| 8π |
| 1 |
| 8π |
| 2h+6-h+6-h |
| 3 |
| 1 |
| π |


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源:安徽省合肥168中学2010届高三第一次月考数学文科学科试题 题型:044
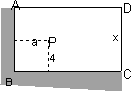
如图,周长为16米的篱笆借助一个墙角围成一个矩形ABCD,在矩形内的一点P处是一棵树,树距离两墙分别为a、4米(0<a<12);若将此树围进去,又使围成的面积最大,如何围法,并求最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com