
(本题满分15分 )已知函数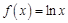 .
.
(1)求函数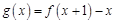 的最大值;
的最大值;
(2)若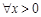 ,不等式
,不等式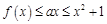 恒成立,求实数
恒成立,求实数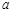 的取值范围;
的取值范围;
(3)若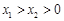 ,求证:
,求证: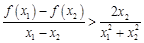 .
.
(1) 在
在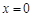 处取得最大值,且最大值为0.(2)
处取得最大值,且最大值为0.(2)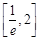 .
(3)见解析。
.
(3)见解析。
【解析】(1)先求出 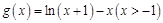 ,然后求导确定单调区间,极值,最值即可.
,然后求导确定单调区间,极值,最值即可.
(2) 本小题转化为 在
在 上恒成立,进一步转化为
上恒成立,进一步转化为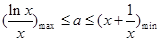 ,然后构造函数
,然后构造函数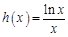 ,利用导数研究出h(x)的最大值,再利用基础不等式可知
,利用导数研究出h(x)的最大值,再利用基础不等式可知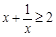 ,从而可知a的取值范围.
,从而可知a的取值范围.
(1)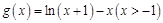 ,则
,则 .…………2分
.…………2分
当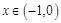 时,
时,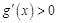 ,则
,则 在
在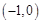 上单调递增;
上单调递增;
当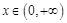 时,
时,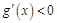 ,则
,则 在
在 上单调递减,
上单调递减,
所以, 在
在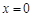 处取得最大值,且最大值为0. ………………………4分
处取得最大值,且最大值为0. ………………………4分
(2)由条件得 在
在 上恒成立. ………………………6分
上恒成立. ………………………6分
设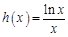 ,则
,则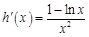 .
.
当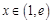 时,
时, ;当
;当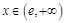 时,
时,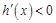 ,所以,
,所以,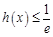 .
.
要使 恒成立,必须
恒成立,必须 .
………………………8分
.
………………………8分
另一方面,当 时,
时,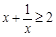 ,要使
,要使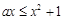 恒成立,必须
恒成立,必须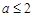 .
.
所以,满足条件的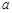 的取值范围是
的取值范围是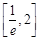 . ………………………10分
. ………………………10分
(3)当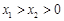 时,不等式
时,不等式 等价于
等价于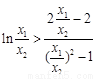 .……12
.……12
令 ,设
,设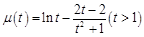 ,则
,则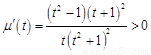 ,
,
 在
在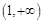 上单调递增,
上单调递增,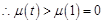 ,
,
所以,原不等式成立. ………………15分


科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试理科数学 题型:解答题
((本题满分15分)
某有奖销售将商品的售价提高120元后允许顾客有3次抽奖的机会,每次抽奖的方法是在已经设置并打开了程序的电脑上按“Enter”键,电脑将随机产生一个 1~6的整数数作为号码,若该号码是3的倍数则顾客获奖,每次中奖的奖金为100元,运用所学的知识说明这样的活动对商家是否有利。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省招生适应性考试文科数学试卷(解析版) 题型:解答题
(本题满分15分)设函数 .
.
(Ⅰ)若函数 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值;
(Ⅱ)若 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
注: 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市十校联合体高三上学期期初摸底文科数学 题型:解答题
(本题满分15分)已知直线 与曲线
与曲线 相切
相切
1)求b的值;
2)若方程 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求
①m的取值范围;
②比较 的大小
的大小
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市十校联合体高三上学期期中考试文科数学 题型:解答题
(本题满分15分)已知抛物线 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 于
于 、
、 两点,
两点, 是线段
是线段 的中点,
的中点,
过 作
作 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点 ,
,
(1)若抛物线 上有一点
上有一点 到焦点
到焦点 的距离为
的距离为 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使 是以
是以 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省六校高三第一次联考文科数学 题型:解答题
(本题满分15分)
已知函数
(1)求 的单调区间;
的单调区间;
(2)设 ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com