练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆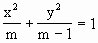(2≤m≤5)，过其左焦点F且斜率为1的直线与椭圆及其准线的交点从左至右的顺序依次为A、B、C、D，记f(m)=||AB|－|CD||

    　　

    (Ⅰ)求f(m)的解析式；

    (Ⅱ)求f(m)的范围．

    答案：
    解析：

    　　解：(1)由题满意知AD方程为：y=x＋1，椭圆准线方程为：x=±m

    　　则A、D两点坐标分别为(－m，1－m)、(m，m＋1)．

    　　联立方程组

    　　消y得：(2m－1)＋2mx－＋2m=0(2≤m≤5)．

    　　设B、C两点坐标分别为

    　　∴

    　　∵

    　　

    　　∴||AB|－|CD||==

    (2≤m≤5)

    　　(2)∵2≤m≤5 ∴

    　　∴


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆E：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）过点P（3，1），其左、右焦点分别为F1，F2，且
    F1P
    •
    F2P
    =-6    ．
    （1）求椭圆E的方程；
    （2）若M，N是直线x=5上的两个动点，且F1M⊥F2N，圆C是以MN为直径的圆，其面积为S，求S的最小值以及当S取最小值时圆C的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＜b＜0)    的左、右焦点分别为F1，F2点A在椭圆C上，
    .
    AF1
    •
    F1F2
    =0，3|
    .
    AF2
    |•|F1A|=-5
    .
    AF2
    •
    F1A
    ，|
    .
    F1F2
    |=2    ，过点F2且与坐标轴不垂直的直线交椭圆于P，Q两点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）线段OF2上是否存在点M（m，0），使得
    .
    OP
    •
    .
    MP
    =
    .
    PQ
    •
    MQ
    ？    若存在，求出实数m 的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (南开中学模拟)已知椭圆(2≤m≤5)，过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D，设．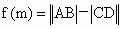

    (1)求f(m)的解析式；

    (2)求f(m)的最值．

    查看答案和解析>>

    科目：高中数学 来源：湖北省期中题 题型：解答题

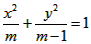    如图，已知椭圆(2≤m≤5)，过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D，设f (m)=||AB|-|CD| |。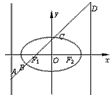

    (1)求f (m)的解析式；　　
    (2)求f (m)的最大、最小值。

    查看答案和解析>>

    同步练习册答案