
分析 由已知得an+1=Sn+1-Sn(n=1,2,3,…),从而nSn+1=2(n+1)Sn,进而得到数列{$\frac{{S}_{n}}{n}$}是首项为1,公比为2的等比数列.由此求出${S}_{n}=n•{2}^{n-1}$,从而能求出an.
解答 解:∵a1=1,an+1=$\frac{n+2}{n}$Sn(n=1,2,3,),
∴a2=$\frac{2+1}{1}$S1=3a1,∴$\frac{{S}_{2}}{2}$=$\frac{4{a}_{1}}{2}$=2,$\frac{{S}_{1}}{1}$=1,
∴$\frac{\frac{{S}_{2}}{2}}{\frac{{S}_{1}}{1}}$=2
又an+1=Sn+1-Sn(n=1,2,3,…),
则Sn+1-Sn=$\frac{n+2}{n}$Sn(n=1,2,3,),
∴nSn+1=2(n+1)Sn,∴$\frac{\frac{{S}_{n+1}}{n+1}}{\frac{{S}_{n}}{n}}$=2(n=1,2,3,…),
故数列{$\frac{{S}_{n}}{n}$}是首项为1,公比为2的等比数列.
∴$\frac{{S}_{n}}{n}={2}^{n-1}$,∴${S}_{n}=n•{2}^{n-1}$,
∴${a}_{1}=1×{2}^{1-1}$=1,
an=Sn-Sn-1=n•2n-1-(n-1)•2n-2=(n+1)•2n-2.
n=1时,上式成立,
∴an=(n+1)•2n-2.
故答案为:(n+1)•2n-2.
点评 本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意构造法及等比数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
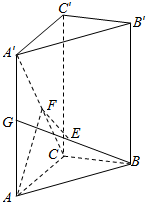 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:
某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com