
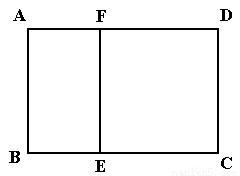
如图,某单位准备修建一个面积为600平方米的矩形场地(图中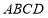 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙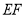 隔开,使得
隔开,使得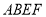 为矩形,
为矩形,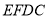 为正方形,设
为正方形,设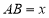 米,已知围墙(包括
米,已知围墙(包括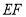 )的修建费用均为800元每米,设围墙(包括
)的修建费用均为800元每米,设围墙(包括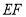 )的修建总费用为
)的修建总费用为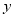 元。
元。
(1)求出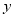 关于
关于 的函数解析式;
的函数解析式;
(2)当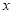 为何值时,设围墙(包括
为何值时,设围墙(包括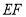 )的的修建总费用
)的的修建总费用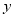 最小?并求出
最小?并求出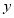 的最小值。
的最小值。
(1)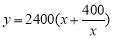
 ;(2)当
;(2)当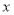 为20米时,
为20米时,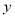 最小.
最小.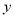 的最小值为96000元.
的最小值为96000元.
【解析】
试题分析:(1)由题意,已知了整个矩形场地的面积,又设了宽AB为x米,所以其长就应为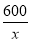 米,从而围墙的长度就为:(
米,从而围墙的长度就为:(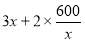 )米,从而修建总费用
)米,从而修建总费用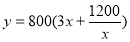 元,只是注意求函数的解析式一定要指出函数的定义域,此题中不仅要
元,只是注意求函数的解析式一定要指出函数的定义域,此题中不仅要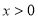 而且还要注意题目中的隐含条件:“中间用围墙
而且还要注意题目中的隐含条件:“中间用围墙 隔开,使得
隔开,使得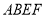 为矩形,
为矩形,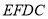 为正方形”从而可知矩形ABCD的长
为正方形”从而可知矩形ABCD的长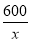 应当要大于其宽x,所以x还应满足:
应当要大于其宽x,所以x还应满足: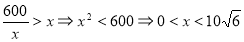 ;(2)由(1)知
;(2)由(1)知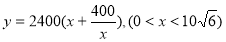 所以可用基本不等式来求y的最小值,及对应的x的值;最后应用问题一定要注意将数学解得的结果还原成实际问题的结果.
所以可用基本不等式来求y的最小值,及对应的x的值;最后应用问题一定要注意将数学解得的结果还原成实际问题的结果.
试题解析:(1)设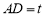 米,则由题意得
米,则由题意得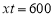 ,且
,且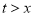 2分
2分
故 ,可得
,可得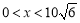 4分
4分
(说明:若缺少“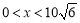 ”扣2分)
”扣2分)
则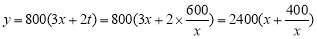 , 6分
, 6分
所以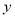 关于
关于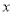 的函数解析式为
的函数解析式为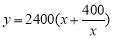
 . 7分
. 7分
(2)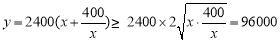 , 10分
, 10分
当且仅当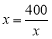 ,即
,即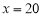 时等号成立. 12分
时等号成立. 12分
故当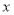 为20米时,
为20米时,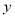 最小.
最小.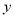 的最小值为96000元. 14分
的最小值为96000元. 14分
考点:1.函数解析式;2.基本不等式.


科目:高中数学 来源:2016届广东省高一下学期期中考试文科数学试卷(解析版) 题型:选择题
在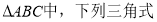 ①sin(A+B)+sinC;②cos(B+C)+cosA;③
①sin(A+B)+sinC;②cos(B+C)+cosA;③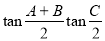
④cos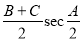 ,其中恒为定值的是 ( )
,其中恒为定值的是 ( )
A.①② B②③ C②④ D③④
查看答案和解析>>
科目:高中数学 来源:2016届广东省汕头市高一下学期期末考试数学试卷(解析版) 题型:选择题
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高 | 160 | 165 | 170 | 175 | 180 |
体重 | 63 | 66 | 70 | 72 | 74 |
根据上表可得回归直线方程 ,据此模型预报身高为172
,据此模型预报身高为172 的高三男生的体重为 ( )
的高三男生的体重为 ( )
A.70.09 B.70.12
B.70.12 C.70.55
C.70.55 D.71.05
D.71.05
查看答案和解析>>
科目:高中数学 来源:2016届广东省梅州市高一上学期质检数学试卷(解析版) 题型:选择题
一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是( )

查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期第一次阶段考试数学试卷(解析版) 题型:选择题
过点 的直线,将圆形区域
的直线,将圆形区域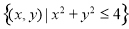 分两部分,使得这两部分的面积之差最大,则该直线的方程为( )
分两部分,使得这两部分的面积之差最大,则该直线的方程为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com