
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于两点
交于两点![]() ,
,![]() .
.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() R,求
R,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,利用圆的弦长公式,列出方程求得
,利用圆的弦长公式,列出方程求得![]() 的值,即可得到直线的方程;
的值,即可得到直线的方程;
(2)当直线![]() 的斜率不存在时,根据向量的运算,求得
的斜率不存在时,根据向量的运算,求得![]() ,当直线
,当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,联立方程组,利用根与系数的关系,以及向量的运算,求得
,联立方程组,利用根与系数的关系,以及向量的运算,求得![]() ,得到答案.
,得到答案.
(1)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,不符合题意;
,不符合题意;
当直线![]() 的斜率存在时,设斜率为
的斜率存在时,设斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() . .
. .
(2)当直线![]() 的斜率不存在时,不妨设
的斜率不存在时,不妨设![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() .
.
当直线![]() 的斜率存在时,设斜率为
的斜率存在时,设斜率为![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,
因为直线![]() 与
与![]() 轴交于点
轴交于点![]() ,所以
,所以![]() .
.
直线![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
由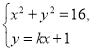 得,
得,![]() ,所以
,所以![]() ,
,![]() ;
;
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以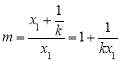 ,
,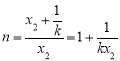 ,
,
所以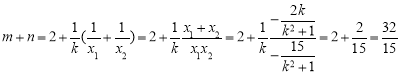 .
.
综上,![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】设函数 f(x)=|x+2|﹣|x﹣3|﹣a
(Ⅰ)当 a=1 时,求函数 f(x)的最大值;
(Ⅱ)若 f(x)≤ ![]() 对任意 x∈R 恒成立,求实数 a 的取值范围.
对任意 x∈R 恒成立,求实数 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
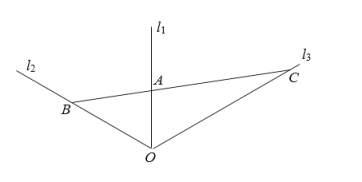
【题目】如图,三条直线型公路![]() ,
,![]() ,
,![]() 在点
在点![]() 处交汇,其中
处交汇,其中![]() 与
与![]() 、
、![]() 与
与![]() 的夹角都为
的夹角都为![]() ,在公路
,在公路![]() 上取一点
上取一点![]() ,且
,且![]() km,过
km,过![]() 铺设一直线型的管道
铺设一直线型的管道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(
上(![]() ,
,![]() 足够长),设
足够长),设![]() km,
km,![]() km.
km.
(1)求出![]() ,
,![]() 的关系式;
的关系式;
(2)试确定![]() ,
,![]() 的位置,使得公路
的位置,使得公路![]() 段与
段与![]() 段的长度之和最小.
段的长度之和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,现采用分层抽样的方法从这些学校中抽取5所学校,对学生进行视力检查.
(1)求应从小学、中学中分别抽取的学校数目;
(2)若从抽取的5所学校中抽取2所学校作进一步数据
①列出所有可能抽取的结果;
②求抽取的2所学校至少有一所中学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人用三段论进行推理:“函数![]() 的导函数
的导函数![]() 的零点即为函数
的零点即为函数![]() 的极值点,函数
的极值点,函数![]() 的导函数的零点为
的导函数的零点为![]() ,所以
,所以![]() 是函数
是函数![]() 的极值点 ”,上面的推理错误的是( )
的极值点 ”,上面的推理错误的是( )
A. 大前提 B. 小前提 C. 推理形式 D. 以上都是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1的棱长为1,点E,F分别是棱D1C1 , B1C1的中点,过E,F作一平面α,使得平面α∥平面AB1D1 , 则平面α截正方体的表面所得平面图形为( )
A.三角形
B.四边形
C.五边形
D.六边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com