练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数，
    （1）  若f(x)在区间[m,m+1]上单调递减，求实数m的取值范围；
    （2）  若f(x)在区间[a,b]（a<b）上的最小值为a，最大值为b，求a、b的值。
    (1)的对称轴为.
    (2)
    故在上单调递增.   
    为方程的两根
    由
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    已知函数.
    （1）若对任意的实数，都有，求的取值范围；
    （2）当时，的最大值为M，求证：；
    （3）若，求证：对于任意的，的充要条件是

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知-，求
    （1）时，的最值。
    2.-1，时，的最值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设是某港口水的深度y（米）关于时间t（时）的函数，其中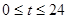，下表是该港口某一天从0时至24时记录的时间t与水深y的关系
    t
    		0
    		3
    		6
    		9
    		12
    		15
    		18
    		21
    		24
    y
    		12
    		15．1
    		12．1
    		9．1
    		11．9
    		14．9
    		11．9
    		8．9
    		12．1
     
    经长期观察，函数的图象可以近似地看成函数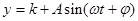的图象，下面的函数中，最能近似表示表中数据间对应关系的函数是      （   ）
    A．     B．
    C．     D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

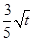    （本题满分12分）销售甲、乙两种商品所得利润分别是P(万元)和Q(万元)，它们与投入资金t(万元)的关系有经验公式P＝，Q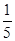＝t．今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x(万元)．
    求：(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式；
    (2)总利润y的最大值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

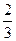    已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
    （I）求f(x)的解析式;
    （II）已知k的取值范围为[,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知y＝f(x)是定义在R上的函数，且f(1)＝1，f′(x)>1，则f(x)>x的解集是(　)
    A．(0,1)B．(－1,0)∪(0,1)
    C．(1，＋∞) D．(－∞，－1)∪(1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知是偶函数，定义域为，则  

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知f(x)＝32x－(k＋1)3x＋2，当x∈R时，f(x)恒为正值，则k的取值范围是

    查看答案和解析>>

    同步练习册答案