Question

【题目】在数列{an}中，a1=1， = + （n∈N*）．
（1）求数列{an}的通项公式；
（2）设bn=1+a （n∈N*），求数列{2nbn}的前n项和Sn ．

Answer 1

【答案】
（1）解：∵ = + ，即 ﹣ = ，

又 = ，

∴{ }是以 为首项，以 为公差的等差数列．

∴ = + （n﹣1）= ，

∴an= ﹣1．

（2）解：bn=1+a = = ．

∴2nbn= ，

∴Sn= + + + +…+ ，①

∴ Sn= + + + +… ，②

① ﹣②得：

Sn= + + + +…+ ﹣

= ﹣

=8﹣ ﹣ =8﹣ ．

∴Sn=16﹣ ．

【解析】（1）移项得 ﹣ = ，故{ }是等差数列，求出此等差数列的通项公式即可得出an；（2）计算bn ， 得出2nbn ， 利用错位相减法求出Sn ．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系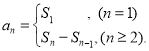；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．