
如图,它是曲柄连杆装置示意图,连杆AC=l,曲柄AB=r,曲柄AB和曲轴BC的角为α.
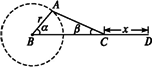
(1)求连杆AC和曲轴BC间的夹角β的正弦.
(2)当α取什么值时,β最大?
(3)求滑块C的位移x.
|
解:(1)在△ABC中,由正弦定理,知sinβ= (2)由(1)知sinβ= ∵0≤β≤ (3)在△ABC中,由余弦定理:BC2=AB2+AC2-2AB·AC·cos∠BAC. ∴BC2=r2+l2-2rlcos(π-α-β)=r2+l2+2rlcos(α+β). ∴BC= ∴位移x=r+l-BC=r+l- 思路解析:由α、β、l、r构成的△ABC中,求β的正弦可让我们想到正弦定理,根据正弦函数的有界性,进而由sinβ的最值利用正弦函数的单调性求出β的最值. |


科目:高中数学 来源:设计必修五数学人教A版 人教A版 题型:044
如图,它是曲柄连杆装置示意图,连杆AC=l,曲柄AB=r,曲柄AB和曲轴BC的角为α.

(1)求连杆AC和曲轴BC间的夹角β的正弦.
(2)当α取什么值时,β最大?
(3)求滑块C的位移x.
查看答案和解析>>
科目:高中数学 来源:训练必修五数学人教A版 人教A版 题型:044
如图,它是曲柄连杆装置示意图,连杆AC=l,曲柄AB=r,曲柄AB和曲轴BC的夹角为α.
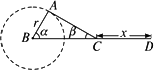
(1)求连杆AC和曲轴BC间的夹角β的正弦值.
(2)当α取什么值时,β最大?
(3)求滑块C的位移x.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1-2(3)-14,它是曲柄连杆装置示意图,连杆AC=l,曲柄AB=r,曲柄AB和曲轴BC的角为α.
(1)求连杆AC和曲轴BC间的夹角β的正弦.
(2)当α取什么值时,β最大?
(3)求滑块C的位移x.

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求连杆AC和曲轴BC间的夹角β的正弦值.
(2)当α取什么值时,β最大?
(3)求滑块C的位移x.

图1-2-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com