
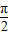 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.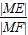 =1时,试问x的值为多少?
=1时,试问x的值为多少?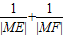 的取值范围.
的取值范围. =1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,利用几何性质即可求出x的值;
=1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,利用几何性质即可求出x的值;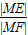 =1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,
=1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,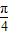 ;
;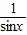 =
=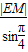 ,得|EM|=
,得|EM|=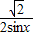 ,x∈(0,
,x∈(0,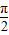 ),
),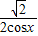 ,x∈(0,
,x∈(0,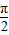 ),
),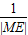 +
+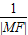 =
=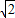 sinx+
sinx+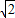 cosx=2sin(x+
cosx=2sin(x+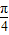 ),
),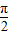 ),∴x+
),∴x+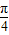 ∈(
∈(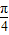 ,
,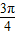 ),即有sin(x+
),即有sin(x+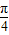 )∈(
)∈(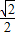 ,1],
,1],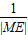 +
+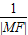 ∈(
∈(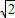 ,2].
,2].

科目:高中数学 来源: 题型:
| π |
| 2 |
| |ME| |
| |MF| |
| 1 |
| |ME| |
| 1 |
| |MF| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 2 |
| lnx |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 2 |
| |ME| |
| |MF| |
| 1 |
| |ME| |
| 1 |
| |MF| |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 2 |
| |ME| |
| |MF| |
| 1 |
| |ME| |
| 1 |
| |MF| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com