
【题目】数列![]() 满足:
满足:![]()
(1)求![]() 的值;
的值;
(2)求证:数列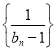 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(3)设![]() 假设
假设![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见详解,
;(2)证明见详解,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据递推公式,进行赋值即可求得;
(2)根据等差数列的定义,用其后一项减去前一项,证明其为常数即可;
(3)先根据![]() 利用裂项求和求得
利用裂项求和求得![]() ,再将恒成立问题转化为二次函数恒成立问题即可.
,再将恒成立问题转化为二次函数恒成立问题即可.
(1)因为![]()
故可得![]()
因为![]() ,根据
,根据![]() ,可解的
,可解的![]() ;
;
由![]() ,可得
,可得![]()
则![]() ,
,
综上:![]() ,
,![]() ,
,![]() .
.
(2)证明:由(1)知:![]()
故![]() ,
,
故数列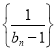 是首项为-4,公差为-1的等差数列,即证.
是首项为-4,公差为-1的等差数列,即证.
故![]() ,解得
,解得![]() .
.
(3)由(2)知![]() ,因为
,因为![]() ,
,
故可得![]()
故![]()
![]()
![]()
![]()
故![]() ,又
,又![]()
故![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,即
恒成立,即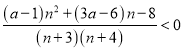 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,
,![]() .
.
当![]() 时,
时,![]() 恒成立,满足题意;
恒成立,满足题意;
当![]() 时,由二次函数的性质可知,显然不成立;
时,由二次函数的性质可知,显然不成立;
当![]() 时,对称轴
时,对称轴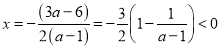
故![]() 在
在![]() 单调递减,要满足题意,只需
单调递减,要满足题意,只需![]() 即可,即
即可,即![]() ,解得
,解得![]() ,
,
又因为![]() ,故
,故![]() .
.
综上当![]() 时,
时,![]() 恒成立.
恒成立.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在第三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有( )
A.12种B.24种C.36种D.48种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁、戊和己6人围坐在一张正六边形的小桌前,每边各坐一人.已知:①甲与乙正面相对;②丙与丁不相邻,也不正面相对.若己与乙不相邻,则以下选项正确的是( )
A.若甲与戊相邻,则丁与己正面相对B.甲与丁相邻
C.戊与己相邻D.若丙与戊不相邻,则丙与己相邻
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .(
.(![]() 且
且![]() )
)
(1)分别判断当![]() 及
及![]() 时函数的奇偶性;
时函数的奇偶性;
(2)在![]() 且
且![]() 的条件下,将(1)的结论加以推广,使命题(1)成为推广后命题的特例,并对推广的结论加以证明.
的条件下,将(1)的结论加以推广,使命题(1)成为推广后命题的特例,并对推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:


(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com