
已知函数 是偶函数.
是偶函数.
(1)求 的值;
的值;
(2)设 ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围。
的取值范围。
(1)- ;(2){a
;(2){a a>1或a=-3}
a>1或a=-3}
【解析】
试题分析:(1)根据偶函数可知f(x)=f(-x),取x=-1代入即可求出k的值;
(2)函数f(x)与g(x)的图象有且只有一个公共点,则方程f(x)=g(x)有且只有一个实根,化简可得2x+ =a•2x?
=a•2x? a有且只有一个实根,令t=2x>0,则转化成方程(a?1)t2?
a有且只有一个实根,令t=2x>0,则转化成方程(a?1)t2? at?1=0有且只有一个正根,讨论a=1,以及△=0与一个正根和一个负根,三种情形,即可求出实数a的取值范围.
at?1=0有且只有一个正根,讨论a=1,以及△=0与一个正根和一个负根,三种情形,即可求出实数a的取值范围.
试题解析:(1)∵函数 f(x)= (
( +1)+kx(k∈R)是偶函数
+1)+kx(k∈R)是偶函数
∴ f(-x)= (
( +1)-kx=
+1)-kx= -kx=
-kx= (4x+1)-(k+1)x=
(4x+1)-(k+1)x= (4x+1)+kx恒成立
(4x+1)+kx恒成立
∴-(k+1)=k,则k=- 4分
4分
(2)g(x)= (a·
(a· -
- a),
a),
函数 f(x)与g(x)的图象有且只有一个公共点,即方程 f(x)=g(x)只有一个解
由已知得 (4x+1)-
(4x+1)- x=
x= (a·
(a· -
- a)
a)
∴
 =
= (a·
(a· -
- a),∴
a),∴ 且
且 =
= 8分
8分
设 。
。
设h(t)=(a-1)t2- at-1,若a-1>0,∵h(0)=-1<0,∴恰好有一正解,a>1满足题意。
at-1,若a-1>0,∵h(0)=-1<0,∴恰好有一正解,a>1满足题意。
若a-1=0,a=1,不满足题意。
若a-1<0,即a<1时, =0的a=-3或a=
=0的a=-3或a= ,
,
当a=-3时t= 满足题意。
满足题意。
当a= 时,t=-2(舍去) 11分
时,t=-2(舍去) 11分
综上:a的取值范围是{a a>1或a=-3} 12分
a>1或a=-3} 12分
考点:对数函数图像与性质的综合应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:选择题
平面 平面
平面 的一个充分条件是
的一个充分条件是
A. 存在一条直线 ,
, 且
且
B. 存在一个平面 ,
, ∥
∥ 且
且 ∥
∥
C. 存在一个平面 ,
, ⊥
⊥ 且
且 ⊥
⊥
D. 存在一条直线 ,
, 且
且 ∥
∥
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
“ ”是“直线
”是“直线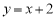 与圆
与圆 相切”的( )
相切”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
抛物线 的准线与双曲线
的准线与双曲线  交于
交于 两点,点
两点,点 为抛物线的焦点,若△
为抛物线的焦点,若△ 为直角三角形,则双曲线的离心率为( )
为直角三角形,则双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试理科数学试卷(解析版) 题型:选择题
某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A.这种抽样方法是一种分层抽样.
B.这种抽样方法是一种系统抽样.
C.这五名男生成绩的方差大于这五名女生成绩的方差.
D.该班级男生成绩的平均数小于该班女生成绩的平均数.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟常考问题8练习卷(解析版) 题型:选择题
已知点A(1,3),B(4,-1),则与向量 同方向的单位向量为( ).
同方向的单位向量为( ).
A.  B.
B. 
C. 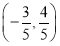 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com