练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

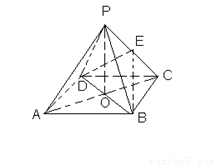
    （本题8分）如图，ABCD是正方形，O是正方形的中心， PO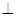底面ABCD，E是PC的中点。

    求证：（1）PA∥平面BDE   （2）平面PAC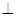平面BDE

     

    【答案】

    见解析。

    【解析】本题主要考查中位线定理、线面平行的判定定理和面面垂直的判定定理．考查立体几何的基本定理和空间想象能力

    （1）先根据中位线定理得到OE∥AP，进而再由线面平行的判定定理可得到PA∥平面BDE．

    （2）先根据线面垂直的性质定理得到PO⊥BD，结合AC⊥BD根据线面垂直的判定定理得到BD⊥平面PAC，从而根据面面垂直的判定定理得到平面PAC⊥平面BDE，得证．

    证明：（1）连结E0

    四边形ABCD为正方形

    O为AC的中点  又E是PC的中点

    EO//PA

    PA//平面BDE                       4分

    （2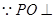）平面ABCD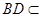，平面ABCD     

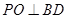
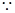    四边形ABCD是正方形       

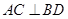
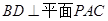     ，又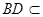平面BDE

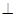    平面PAC平面BDE                 4分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011年安徽省师大附中高一第一学期期中考试数学 题型：解答题

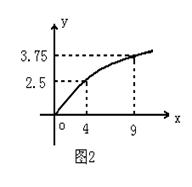
    (本题8分)某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位是万元）
    （1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式
    （2）该企业已筹集到10万元资金，并全部投入A，B两种产品的生产，问：怎样分配这10万元投资，才能是企业获得最大利润，其最大利润约为多少万元（精确到1万元）.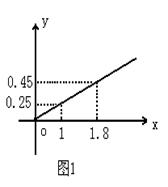

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省嘉兴市八校高二上期中联考理科数学试卷（解析版） 题型：解答题

    （本题8分）如图，已知点A(2,3), B(4,1)，△ABC是以AB为底边的等腰三角形，点C在直线l：x－2y＋2＝0上．

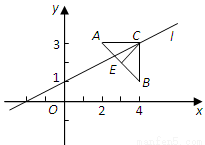
    （Ⅰ）求AB边上的高CE所在直线的方程；

    （Ⅱ）求△ABC的面积．

     

    查看答案和解析>>

    科目：高中数学 来源：2011年安徽省高一第一学期期中考试数学 题型：解答题

    (本题8分)某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位是万元）

    （1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式

    （2）该企业已筹集到10万元资金，并全部投入A，B两种产品的生产，问：怎样分配这10万元投资，才能是企业获得最大利润，其最大利润约为多少万元（精确到1万元）.

     

    查看答案和解析>>

    科目：高中数学 来源：2010年海南省高一期中考试数学试卷 题型：解答题

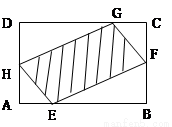
    （本题满分8分）如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB＝a（a>2），BC＝2，且AE＝AH＝CF＝CG，设AE＝x，绿地面积为y．

    (Ⅰ)写出y关于x的函数关系式，并指出这个函数的定义域；

    (Ⅱ)当AE为何值时，绿地面积最大？

     

    查看答案和解析>>

    科目：高中数学 来源：2010年山东省北校区高二上学期第一次月考数学卷 题型：解答题

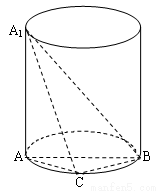
    （本题满分8分）如图，A1A是圆柱的母线，AB是圆柱底面圆的直径， C是底面圆周上异于A，B的任意一点，A1A= AB=2.

    （Ⅰ）求证: BC⊥平面A1AC；

    （Ⅱ）求三棱锥A1-ABC的体积的最大值.

     

     

     

    查看答案和解析>>

    同步练习册答案