
(本题8分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
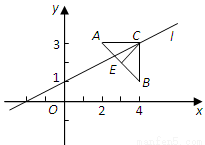
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.
(Ⅰ)x-y-1=0.(Ⅱ)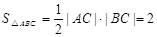 .
.
【解析】(I)先由AB的斜率求出CE的斜率,因为AC=BC,所以E为AB的中点,进而写出点斜式方程,再化成一般式方程.
(II)由直线l的方程和CE的方程联立解方程组可解出点C的坐标,然后利用两点间的距离公式可求出CE和AB的长度,再利用面积公式求值即可.
解:(Ⅰ)由题意可知,E为AB的中点,∴E(3,2),……………………1分
且 ,……………………………………………………1分,
,……………………………………………………1分,
∴CE:y-2=x-3,即x-y-1=0.………………………………2分
(Ⅱ)由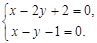 得C(4,3),…………………………………1分
得C(4,3),…………………………………1分
∴|AC|=|BC|=2,AC⊥BC,…………………………………………1分
∴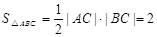 .………………………………………2分
.………………………………………2分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011-2012学年上海市长宁区高三4月教学质量检测(二模)理科数学试卷(解析版) 题型:解答题
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。
如图,已知四棱锥P—ABCD,底面ABCD为矩形, ,PA
,PA 平面ABCD, E,F分别是BC,PC的中点。
平面ABCD, E,F分别是BC,PC的中点。
(1)求异面直线PB与AC所成的角的余弦值;
(2)求三棱锥 的体积。
的体积。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市崇明县高三第一学期期末考试数学 题型:解答题
(本题18分,第(1)小题4分;第(2)小题6分;第(3)小题8分)
如图,已知椭圆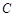 :
: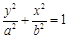
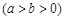 过点
过点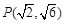 ,上、下焦点分别为
,上、下焦点分别为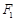 、
、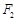 ,
,
向量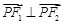 .直线
.直线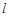 与椭圆交于
与椭圆交于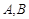 两点,线段
两点,线段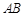 中点为
中点为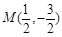 .
.
(1)求椭圆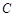 的方程;
的方程;
(2)求直线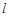 的方程;
的方程;
(3)记椭圆在直线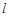 下方的部分与线段
下方的部分与线段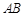 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为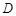 ,若曲线
,若曲线
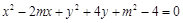 与区域
与区域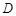 有公共点,试求
有公共点,试求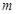 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013届内蒙古呼伦贝尔市高二上学期第一次综合考试理科数学 题型:解答题
(本题满分8分)如图,已知△ABC在平面α外,它的三边所在直线分别交平面α于点P、Q、R,求证:P、Q、R三点共线.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本题18分,第(1)小题4分;第(2)小题6分;第(3)小题8分)
如图,已知椭圆E:![]()
![]() ,焦点为
,焦点为![]() 、
、![]() ,双曲线G:
,双曲线G:![]()
![]() 的顶点是该椭圆的焦点,设
的顶点是该椭圆的焦点,设![]() 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线![]() 、
、![]() 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形![]() 的周长等于
的周长等于![]() ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为![]() .
.
(1)求椭圆E与双曲线G的方程;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,探求
,探求![]() 和
和![]() 的关系;
的关系;
 (3)是否存在常数
(3)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,试求出
恒成立?若存在,试求出![]() 的值;若不存在,
的值;若不存在,
请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com